How to Calculate Relative Uncertainty

Introduction

Relative uncertainty is a concept that has been around for quite some time. It is commonly referenced in many documents but rarely covered in any detail.

While relative uncertainties may seem simple, there are more use cases than just percent uncertainty such as parts per million uncertainty and uncertainty relative to a measured quantity. Additionally, I receive a lot of questions about this topic. So, I decided to answer many of them here.

In this guide, you will learn all about relative uncertainty, including:

 
Plus, you will see plenty of examples of how accredited laboratories use it in their certificates and scope of accreditation.

If this topic interests you, then keep reading. There is a lot of good information in this guide.

What is Relative Uncertainty

According to the Vocabulary in Metrology (i.e. VIM), relative uncertainty is the measurement uncertainty divided by the absolute value of the measured quantity value.

In simple terms, it is the ratio of the uncertainty to the measured quantity.

Depending on the use case, the uncertainty could be a standard uncertainty or an expanded uncertainty.

Look at the image below to see a sample from the GUM or JCGM 100:2008. It provides an example of a standard uncertainty relative to the measured quantity.

Why Use Relative Uncertainties

There are only a few reasons why you would use relative uncertainties. They include;

1. It makes the measurement uncertainty easier to understand,
2. It makes the measurement uncertainty easier to apply to similar quantities,
3. It is common practice for your industry, or
4. It is common practice for your measurement function.

In most cases, it is used to simplify measurement uncertainty calculations, especially for complex measurement functions. It is easier to understand or apply a percent (%) uncertainty or parts-per-million (PPM) uncertainty than an absolute uncertainty.

In other situations, using it is common practice:

• Chemical concentrations: %CV or %RSD is common
• Dimensional measurements: use quantity related values such as L, DL, D are common
• Mechanical measurements: W, %, or micro-units per unit is common
• Electrical measurements: E, %, or micro-units per unit is common
• Thermodynamic measurements: T, %, or micro-units per unit is common
• Most other measurement functions use % or micro-units per unit

However, you should be careful. Relative uncertainties are not appropriate for some evaluations. Additionally, they may cause you to overstate or understate your expanded uncertainty if they are relative to your input quantity (i.e. your uncertainty contributor) instead of your output quantity (i.e. the uncertainty contributed to your measurement result).

If they are relative to your input quantity, check to see if you need to use a sensitivity coefficient. This is common for complex formulas and equations.

Types of Relative Uncertainty

There are several types of relative uncertainties commonly used by accredited laboratories. In this section, you will learn about:

1. Percent Uncertainty,
2. Parts Per Million Uncertainty, and
3. Uncertainty Relative to the Measured Quantity

Percentage Uncertainty

Percentage is the most used relative uncertainty. It is easy to understand, easy to calculate, and has a variety of applications.

If you look at a lot of scopes of accreditation and equipment datasheets, you will see the following examples of percent uncertainty.

• % of reading
• % of Full Scale
• % of Full Span
• % RSD
• % CV

Parts Per Million Uncertainty

Parts per million is the second most used relative uncertainty. Similar to percentage, it is easy to understand, easy to calculate, and has a variety of applications.

According to ILAC P14, you are not allowed to use the abbreviation “PPM.” However, there are plenty of examples for using a part per million uncertainty. Just look at laboratory scopes of accreditation.

• Parts per 10⁶
• Parts in 10⁶
• x 10^-n
• Micro unit per unit (e.g. µV/V)

Uncertainty Relative to the Quantity Measured

Using an uncertainty that is relative to the measured quantity is very common for dimensional and mechanical laboratories.

Instead of using percentage or parts per million, it is based on the measured parameter such as:

• Length (L),
• Diagonal Length (DL),
• Diameter (D),
• Weight (W or Wt), or
• Temperature (T)

All you need to do is look at the scope of accreditation for several accredited laboratories to see some examples.

How to Calculate Relative Uncertainty

When discussing relative uncertainties, the most common questions are about:

1. Calculating relative uncertainties,
2. Converting them to other relative uncertainties, or
3. Calculating uncertainty with relative uncertainties

In this section, you will learn how to calculate and convert relative uncertainties.

Calculate Percentage Uncertainty

Percent uncertainty is the ratio of the expanded uncertainty to the measured quantity on a scale relative to 100%.

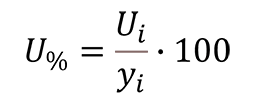
Where,
U_i = expanded uncertainty; 95% where k=2
y_i = measured result or quantity
U_% = expanded uncertainty in percentage

How to Calculate Percent Uncertainty

To calculate percent uncertainty, follow the instructions below:

1. Divide the uncertainty by the measured quantity, and
2. Multiply the result of Step 1 by 100.

Convert Percent Uncertainty to Absolute Uncertainty

To convert percent uncertainty to an absolute uncertainty, follow the instructions below:

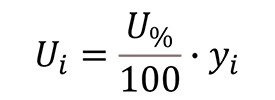
1. Divide the percent uncertainty by 100, and
2. Multiply the result of Step 1 by the measured quantity.

Convert Percent Uncertainty to Part Per Million Uncertainty

To convert percent uncertainty to a parts per million uncertainty, follow the instructions below:

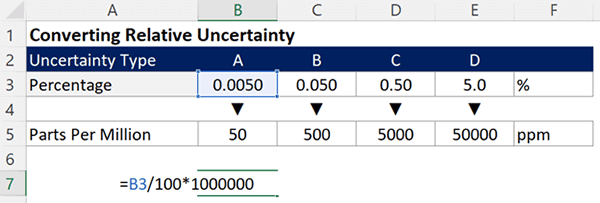
When your percent uncertainty is too small (i.e. typically smaller than 0.01%), you may want to convert it to a parts per million uncertainty.

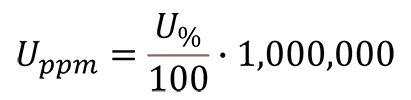
1. Divide the percent uncertainty by 100;
2. Multiply the result of Step 1 by 1,000,000.

Shortcut: Multiply the percent uncertainty by 10,000.

Calculate Parts Per Million Uncertainty

Parts per million uncertainty is the ratio of the expanded uncertainty to the measured quantity on a scale relative to one million or 1000000.

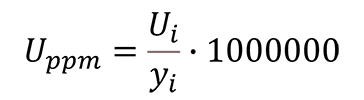
Where,
U_i = expanded uncertainty; 95% where k=2
y_i = measured result or quantity
U_ppm = expanded uncertainty in parts per 10^6

How to Calculate Parts Per Million Uncertainty

To calculate parts per million uncertainty, follow the instructions below:

1. Divide the uncertainty by the measured quantity,
2. Multiply the result of Step 1 by 1,000,000.

Convert Part Per Million Uncertainty to Absolute Uncertainty

To convert parts per million uncertainty to an absolute uncertainty, follow the instructions below:

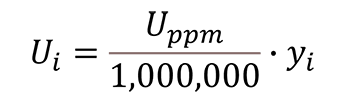
1. Divide the parts per million uncertainty by 1,000,000;
2. Multiply the result of Step 1 by the measured quantity.

Convert Part Per Million Uncertainty to Percent Uncertainty

To convert parts per million uncertainty to a percent uncertainty, follow the instructions below:

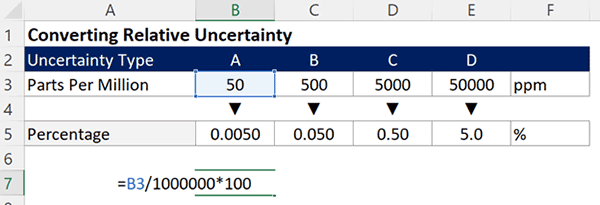
When your parts per million uncertainty becomes too large (i.e. typically larger than 1,000ppm), you may want to convert it to a percent uncertainty.

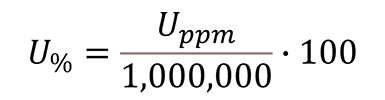
1. Divide the parts per million uncertainty by 1,000,000;
2. Multiply the result of Step 1 by 100.

Shortcut: Divide the parts per million uncertainty by 10,000.

Calculate Uncertainty Relative to Measured Quantities

Uncertainty relative to a measured quantity is the ratio of the expanded uncertainty to the measured quantity on a scale relative to the units of measurement the uncertainty will be reported.

The difference with this calculation is the scale multiplier which is determined based on how the uncertainty will be reported in comparison to the measured quantity.

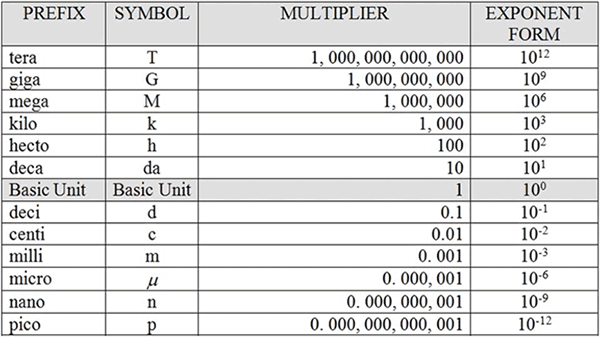
For example, measurement results for length are commonly reported in inches or millimeters. However, the expanded uncertainty is typically reported in micro-inches or micrometers. Therefore, we need to use a scale multiplier (based on SI Prefixes) to ensure that the relative uncertainty component is correct.

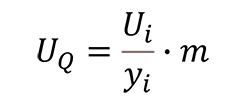
Where,
U_i = expanded uncertainty; 95% where k=2
y_i = measured quantity
m = scale multiplier
U_Q = uncertainty relative to the measured quantity
 
Use the table below to determine which scale multiplier you should use to calculate your uncertainty.

Reporting Relative Uncertainty

Reporting relative uncertainties is common for some people but not for others. In this section, you will see several examples of it reported in scopes of accreditation and certificates.

Relative Uncertainty in Scopes of Accreditation

In this section, you will find examples of laboratories reporting relative uncertainties in their scopes of accreditation. Some sections may have more examples that others. The goal is to provide a variety of use cases that you can use in your own scope of accreditation.

Percentage Uncertainty

In the image below, you will see how Morehouse Instrument Company uses percent uncertainty in their scope of accreditation.

In the image below, you will see how Accurate Calibration uses percent uncertainty in their scope of accreditation. Their scope includes both:

• % of reading, and
• % of indicated value

In the image below, you will see how Huntington Ingalls uses percent uncertainty in their scope of accreditation. Their scope includes both:

• % of reading, and
• % of Full Scale

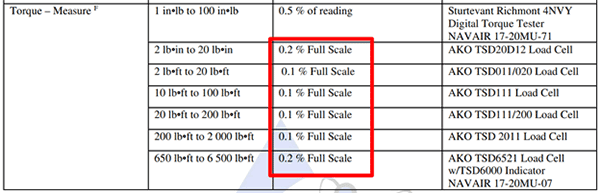
In the image below, you will see how Dick Munns uses percent uncertainty in their scope of accreditation. Their scope includes both:

• % of reading, and
• % of Full Scale

Parts Per Million Uncertainty

In the image below, you will see how Keysight Technologies uses parts per million uncertainty in their scope of accreditation.

In the image below, you will see how ACR Technical Services uses parts per million uncertainty in their scope of accreditation.

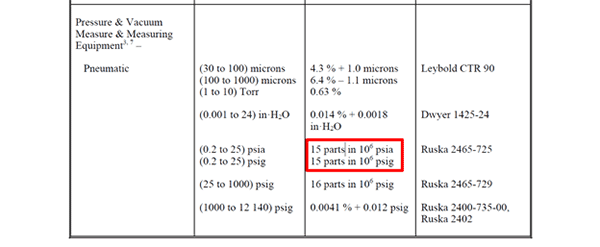
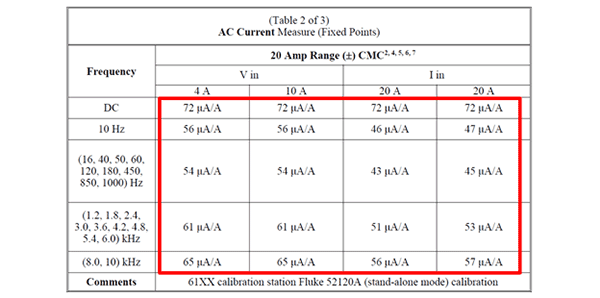
In the image below, you will see how Fluke Everett Service Center uses parts per million uncertainty in their scope of accreditation.

Uncertainty Relative to a Measured Quantity

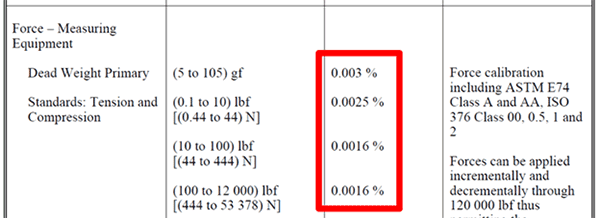
In the image below, you will see how Morehouse Instrument Company uses a CMC uncertainty relative to a measured quantity in their scope of accreditation.

This CMC uncertainty is relative the applied force (F).

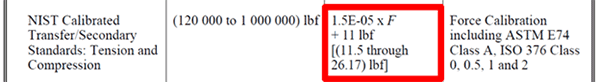
In the image below, you will see how AA Jansson uses a CMC uncertainty relative to a measured quantity in their scope of accreditation.

This CMC uncertainty is relative the measured length (L).

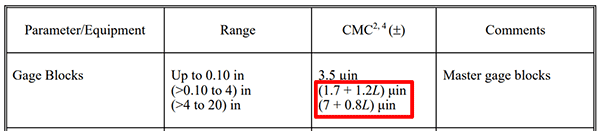
This CMC uncertainty is relative the measured length (L) and temperature (T).

In the image below, you will see how AA Jansson uses a CMC uncertainty relative to a measured quantity in their scope of accreditation.

This CMC uncertainty is relative the measured diameter (D).

This CMC uncertainty is relative the measured diagonal length (DL).

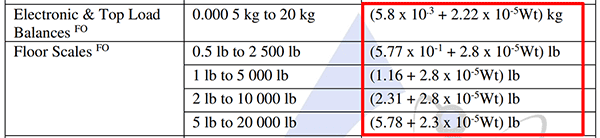
In the image below, you will see how AAA Scale Company uses a CMC uncertainty relative to a measured quantity in their scope of accreditation.

This CMC uncertainty is relative the applied weight (Wt).

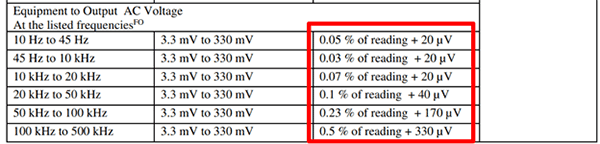
In the image below, you will see how Keysight Technologies uses a CMC uncertainty relative to a measured quantity in their scope of accreditation.

This CMC uncertainty is relative the measured time interval (TI).

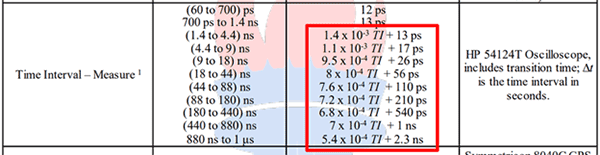
This CMC uncertainty is relative the sourced pulse width (Width).

Relative Uncertainty in Certificates

In this section, you will find examples of laboratories reporting relative uncertainties in their accredited certificates. Some sections may have more examples that others. The goal is to provide a variety of use cases that you can use in your own certificates.

Percentage Uncertainty

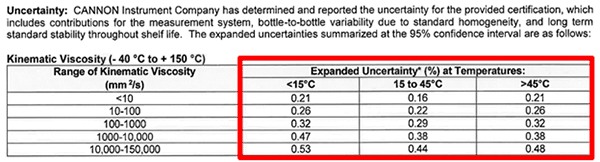
In the image below, you will see how Cannon Instrument Company reports a percent uncertainty in their certificates.

In the image below, you will see how LACO Technologies reports a percent uncertainty in their certificates.

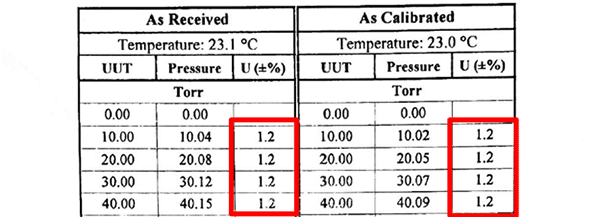
In the image below, you will see how Instron reports a percent uncertainty in their certificates.

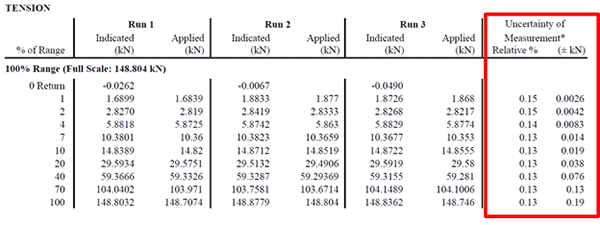
In the image below, you will see how Trescal reports a percent uncertainty in their certificates.

Parts Per Million Uncertainty

In the image below, you will see how Fluke Everett Service Center uses parts per million uncertainty in their calibration certificates.

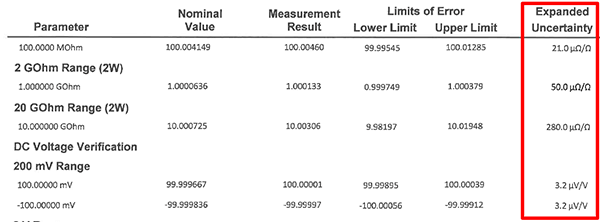
In the image below, you will see how Fluke Phoenix reports a parts per million uncertainty in their certificates.

In the image below, you will see how Tektronix reports a parts per million uncertainty in their certificates.

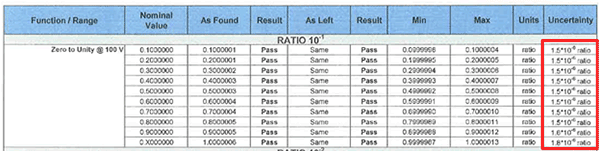
Uncertainty Relative to a Measured Quantity

In the image below, you will see how Master Gage & Tool reports uncertainty relative to a measured quantity in their certificates.

In the image below, you will see how A.A. Jansson reports uncertainty relative to a measured quantity in their certificates.

Conclusion

Relative uncertainty can be a convenient way to report measurement uncertainty that is easy for many people understand and apply to their measurement scenarios.

In this guide, you should have learned:

1. What is it,
2. Why you should use it,
3. How to calculate it, and
4. How to report it.

The information in this guide should be helpful if you need help with relative uncertainties. If you have a question that is not answered in this guide, let me know and we will have it added to this article.