Introduction
Calculating measurement uncertainty is not easy. In fact, I speak with people every day who are having problems with estimating uncertainty. Therefore, I decided to put together this guide disclosing my exclusive seven step process to calculating measurement uncertainty.
In this guide, you will learn how to calculate measurement uncertainty in seven easy steps. Also, you will learn what information you need to calculate uncertainty, how to identify contributors to uncertainty, and how to evaluate your calculations to prevent overestimating or underestimating uncertainty. Furthermore, I will share with you some of my exclusive tips to help you calculate uncertainty like a pro.
Now, this guide is not a complete “how to” manual. Nor, will it answer all of your questions. Instead, it should be used as a quick reference guide to simplify the uncertainty estimation process into seven steps and learn some of my personnel secrets used when I calculate uncertainty.
So, read this guide and use my advice to help you calculate uncertainty. If you have questions, make sure to contact me. Additionally, feel free to use this guide to help you write an uncertainty procedure for your laboratory.
Click here to download the simple uncertainty calculator for free!
How to Calculate Measurement Uncertainty
Estimating measurement uncertainty can be a difficult task. Especially, since most measurement uncertainty guides do not give you a process or procedure.
Therefore, I developed a seven-step process that you can use every time you estimate measurement uncertainty. Just follow the steps below to when you need to create an uncertainty budget.
- Specify the Measurement Process
- Identify Sources of Uncertainty
- Quantify Sources of Uncertainty
- Characterize Sources of Uncertainty
- Convert Uncertainties to Standard Deviations
- Calculate the Combined Uncertainty
- Calculate the Expanded Uncertainty
- Evaluate Your Uncertainty Budget
Step 1. Specify the Measurement Process and Equation
Before you dive in and begin calculating uncertainty, it is best to have a plan. The first part of your plan should be to identify the measurement process or system that you wish to evaluate.
This will help you frame your uncertainty analysis and focus your attention on what matters most.
How to Specify the Measurement Process
To specify the measurement process, follow the instructions below:
- Select the test or measurement function to evaluate.
- Select the measurement method or procedure to be used.
- Select the equipment that will be used.
- Select the desired range of the measurement function.
- Determine the test-points to be evaluated.
Where applicable, identify the mathematical equation that characterizes the measurement function.
Need More Help
If you are having trouble with this process, try answering the following questions:
- What am I measuring?
- How will I measure it?
- What method will I use?
- What equipment will I need?
- What is the range (e.g. min and max) of my measurement capability?
- What are my target test-points?
After answering the questions above, use your answers to identify what measurement process you are evaluating. Then, add that information to your uncertainty budget. Take a look at the image below.
Once you have outlined what you will be evaluating, you can move on to the next step.

What About Indirect Measurements?
If you are performing indirect measurements that require you to calculate your measurement results, then you should evaluate the equation used to determine your measurement result. Each variable in the equation will have its own uncertainty that will directly affect the uncertainty associated with the calculated measurement result.
To help you out, think of using dead weight testers or calibrating torque transducers and standard resistors. Each one of these measurement processes require you to use an equation to calculate a result for comparison purposes. To estimate uncertainty, you will want to break down the equation and evaluate the uncertainty of each variable in the equation.
If you want to learn more about specifying the measurement function and process for your uncertainty analysis, check out this guide:
Step 2: Identify and Characterize the Uncertainty Sources
Now that you have determined the measurement process that you are going to evaluate, you need to identify the factors that influence uncertainty in measurement results.
This process is not typically easy and can be very frustrating. So, stay calm, be patient, and keep researching. You may be surprised by how many influences can affect your measurement results.
Before you begin, I recommend that you find a book or guide on the measurement process you are evaluating. Physics, Chemistry, and Engineering textbooks can come in handy for understanding background and detailed information about your measurement process. If new textbooks are too expensive, you should be able to buy reasonably priced used books on websites like eBay, Amazon, or Chegg.
Other resources that you may want to consider are ASTM and ISO methods. However, if you like free resources (like I do), you may want to search National Metrology Institute websites, such as NIST, NPL, and BIPM. They may have downloadable guides related to your specific measurement processes.
Finding Sources of Uncertainty
Finding sources of uncertainty can be difficult. It requires a lot of time and effort to conduct research. It is the most time-consuming process when evaluating measurement uncertainty.
Based on my experience, finding factors that influence uncertainty typically requires 50% of the time you spend estimating uncertainty. Take a look at the graph below to see how you will typically spend your time estimating uncertainty.
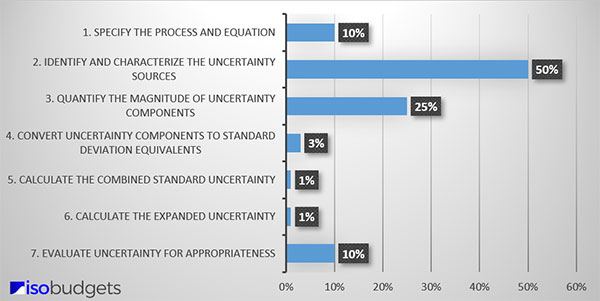
However, if you spend time evaluating your process and conducting research, you should be able to identify several sources of uncertainty for your analysis. Afterward, make a list of these items. You will attempt to quantify them later.
How to Find Sources of Uncertainty
To find sources of uncertainty for your analysis, follow steps listed below:
- Evaluate the test method, calibration procedure, or measurement process.
- Evaluate the measurement equations (if available).
- Evaluate the equipment, reference standards, and reagents.
- Identify the minimum required sources of uncertainty.
- Research various sources of information.
- Consult an expert.
Best Places to Find Sources of Uncertainty
When you need to find sources of uncertainty, it helps to have a list of available resources.
Below is a list of places, including links, that you can use to help you find sources of uncertainty.
- Manufacturer Manuals
- Manufacturer Datasheets
- White Papers
- Technical Notes & Guides
- Conference Papers
- Textbooks
- NIST Special Publications 250 Series
- NIST Internal Reports
- NIST Journal of Research
- NPL Good Practice Guides
- BIPM Publications
- MSL Technical Guides
- EURAMET Calibration & Technical Guides
- Metrologia
- CalLab Magazine
- NCLSI Measure Magazine
Measurement Functions with Equations
If your measurement function includes equations, then the process to estimate uncertainty is a little different. You will want to identify each variable in the equation and think about what influences each variable.
For example, if you are evaluating the calibration of a torque transducer, you will first write out the equation.

When you evaluate the equation further, you begin to account for other factors that influence the equation. In this example, we begin to consider the radius of the torque arm and cable, the mass of the weights and pan, and the local gravity. If needed, we can evaluate the equation even further to account for more influences and increase the complexity of your uncertainty analysis.

Now that you have identified the equation and the variables, you can start to research what factors may cause changes or variations to each variable. Using the example above, think about how temperature variations can cause thermal linear expansion or contraction of the arm radius, and how it can affect air density which affects air buoyancy correction that can vary the magnitude of applied force.
As you can see, evaluating equations can help you find sources of uncertainty. While this process may seem easy, it can become quite difficult depending on the complexity of the equation. Knowing the rules for the propagation of uncertainty can come in handy in step 5.
Measurement Functions without Equations
Most of the measurement functions that you evaluate will not have equations. So, you will need to evaluate the measurement process to find the factors that influence measurement uncertainty.
Start by evaluating the core elements of the measurement process, including the:
- Method,
- Equipment,
- Personnel,
- Environment,
- Unit Under Test, and
- Results
By evaluating these categories, you will find sources of uncertainty that influence measurement results.
Take a look at the table below. Start breaking down each category to see what you find.

You may get lucky and find a paper or guide with a cause and effect (a.k.a. fishbone) diagram or an uncertainty budget already prepared with information applicable to your uncertainty analysis.
The main thing that you must do to find sources of uncertainty is to investigate and research.
To learn more about finding sources of measurement uncertainty, check out this guide:
Step 3. Quantify the Magnitude of Uncertainty Components
Before calculating measurement uncertainty, you must first determine the magnitude of each contributing factor. To accomplish this, you may need to perform some data reduction and analysis.
How to Quantify Uncertainty
To quantify uncertainty, you need to follow the four steps below:
- Collect Information and Data
- Evaluate and Select the Right Data
- Analyze the Data
- Quantify Uncertainty Components
Collect Information and Data
To get started, you need to collect information and data related to your uncertainty analysis. You should have found a lot most of this information in Step 2.
Take a look at the list below and gather the following items. You will need them to quantify sources of uncertainty.
- Last 3 Calibration Reports
- Repeatability and Reproducibility (R&R) Studies
- Method or Procedure
- Experiment Results
- Manufacture Manuals and Specifications
- Technical Documents and Guides
- Published papers, studies, journal articles, etc.
Using the items in the list above, you should be able determine how much uncertainty is contributed from each source. If you need help, you can contact me for additional guidance or hire me to analyze the data for you.
Evaluate Information and Select the Right Data
Next, you need evaluate the information that you have and find data that you will use for estimating uncertainty. You need to find data related to your uncertainty analysis and eliminate everything else from consideration.
This should include information and data related to your:
- measurement function,
- measurement range, and
- test-point.
Analyze the Data
Then, analyze the data that you have using appropriate methods of analysis to find the magnitude of each uncertainty component. You can analyze data in many ways, so choose methods that are appropriate for the data you are analyzing.
If you need help, get a quality statistics textbook or check the free NIST SEMATECH Engineering Statistics Handbook. You can also check out some of my guides on quantifying sources of uncertainty.
Quantify Uncertainty Components
Finally, use your results to quantify each uncertainty component and add the values to your uncertainty budget or uncertainty calculator.
You can add the uncertainty and unit of measurement directly into your uncertainty budget.

Or, you can add uncertainties, their unit of measurement, and a sensitivity coefficient to your uncertainty budgets. The option is yours.

People use different techniques, and that is okay. Just make sure that you are able to explain where your data came from and the way it is evaluated. I recommend adding detailed notes to your uncertainty budgets. It will help you remember how you did it and why.
Sources of Uncertainty
Below, you will see a list of uncertainty components that you should include in every uncertainty budget. Many of these factors are required by section 6 of the A2LA R205 requirements document. While this is not a requirement for everyone, I like their list of minimum required uncertainty contributors and have decided to use them in each one of my uncertainty analyses.
Additionally, I prefer to include more sources of uncertainty in my budgets since I find them to typically be significant. The additional sources I like to consider are long-term stability, bias, and drift.
Here is my list of the minimum recommended sources of uncertainty to include in every uncertainty budget.
- Repeatability
- Reproducibility
- Stability
- Bias
- Drift
- Resolution
- Reference Standard Uncertainty
- Reference Standard Stability
- Other Significant Contributors
Repeatability
Repeatability is an evaluation of the variability in your measurement process under similar conditions.
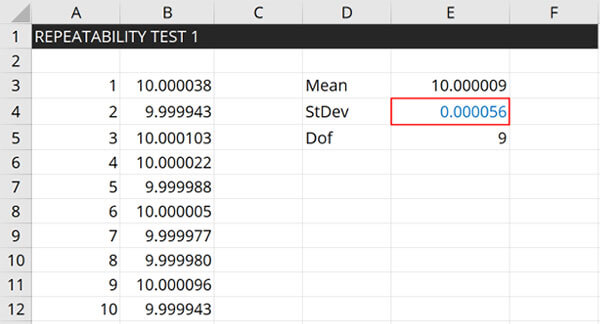
How to Calculate Repeatability
Follow these instructions to calculate repeatability:
- Repeat a measurement ‘n’ number of times
- Record the results of each measurement.
- Calculate the standard deviation.
Reproducibility
Reproducibility is an evaluation of the variability in your measurement process under different conditions.
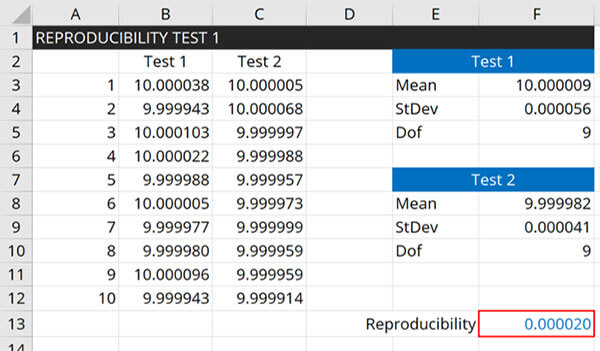
How to Calculate Reproducibility
Follow these instructions to calculate reproducibility:
- Perform a Repeatability Test.
- Calculate the mean of average.
- Change a variable and repeat the Repeatability Test
- Calculate the mean or average.
- Calculate the standard deviation of the test averages.
Stability
Stability is an evaluation of the variability in your measurement process over time.
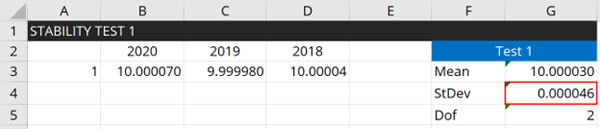
How to Calculate Stability
Follow these instructions to calculate stability:
- Review your last 3 calibration reports.
- Record the results from each calibration report.
- Calculate the standard deviation of the calibration results.
Bias
Bias is an evaluation of the systematic error in your measurement process.

How to Calculate Bias
Follow these instructions to calculate bias:
- Review your latest calibration report.
- Find the As Left value or measurement result.
- Find the Nominal value or standard value.
- Calculate the difference.
Drift
Drift is an evaluation of the systematic change in your measurement process or system over time.
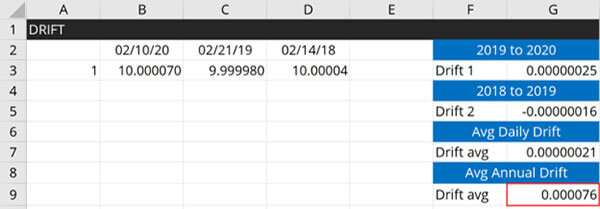
How to Calculate Drift
Follow these instructions to calculate drift:
- Review your last 3 calibration reports.
- Record the results from each calibration report.
- Record the date each calibration was performed.
- Calculate the average daily drift rate.
- Multiply the average daily drift rate by your calibration interval (in days).
Resolution
Resolution is an evaluation of the smallest incremental change observed in your measurement process or system.

How to Find Resolution
Follow these instructions to find resolution:
- Look at your measurement system or equipment.
- Find the least significant digit.
- Observe the smallest incremental change.
Reference Standard Uncertainty
Reference Standard Uncertainty is the traceable uncertainty associated with calibration of equipment or reference materials used in your measurement process.
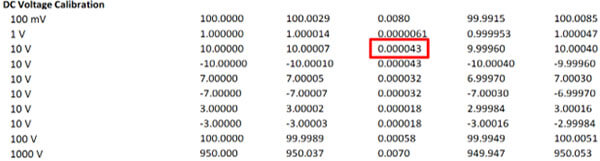
How to Calculate Reference Standard Uncertainty
Follow these instructions to find reference standard uncertainty:
- Review your latest calibration report.
- Find the reported estimate of measurement uncertainty.
Reference Standard Stability
Reference Standard Stability is an evaluation of the variability in your Reference Standard Uncertainty over time.
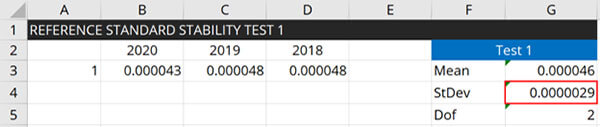
How to Calculate Reference Standard Stability
Follow these instructions to calculate reference standard stability:
- Review your last 3 calibration reports.
- Record the uncertainty estimate from each calibration report.
- Calculate the standard deviation.
Other Significant Contributors
Make sure to include any other significant contributors to measurement uncertainty. A significant contributor is considered a source of uncertainty that contributes 5% or more to the total combined standard uncertainty.
To learn more about sources of uncertainty and how to quantify them, check out these guides:
- 8 Sources of Uncertainty to include in Every Uncertainty Budget
- Linearity Uncertainty
- Hysteresis Uncertainty
- Uncertainty Due to Thermal Expansion
See How We Can Help Your Lab Get ISO/IEC 17025:2017 Accredited
- Uncertainty Budgets – let us estimate uncertainty for you.
- Custom QMS – we’ll create your quality manual, procedures, lists, and forms.
- Training – get online training that teaches you how to estimate uncertainty.
Step 4: Characterize Sources of Uncertainty
Now that you identified and quantified your sources of uncertainty, your next step will be to characterize each factor by uncertainty type and probability distribution.
How to Characterize Sources of Uncertainty
To characterize your sources of uncertainty, perform the following tasks below:
- Categorize each source of uncertainty: Type A or Type B,
- Assign a probability distribution to each uncertainty component.
Uncertainty Types
The first step to characterizing your uncertainty components is to categorize them as either Type A or Type B. Read the sections below to learn the difference between Type A and Type B uncertainty.
Type A Uncertainty
According to the Vocabulary in Metrology (VIM), Type A uncertainty is an “evaluation of a component of measurement uncertainty determined by a statistical analysis of measured quantity values obtained under defined measurement conditions.”
Type B Uncertainty
According to the Vocabulary in Metrology (VIM), Type B uncertainty is an “evaluation of a component of measurement uncertainty determined by means other than a Type A evaluation of measurement uncertainty.”
How to Pick an Uncertainty Type
If you are not sure which uncertainty type you should pick, ask yourself the following questions:
1. Did you collect the data yourself via testing and experimentation?
- If YES, go to question 2
- If No, choose Type B
2. Is the data older than 1 year?
- If YES, choose Type B
- If No, choose Type A
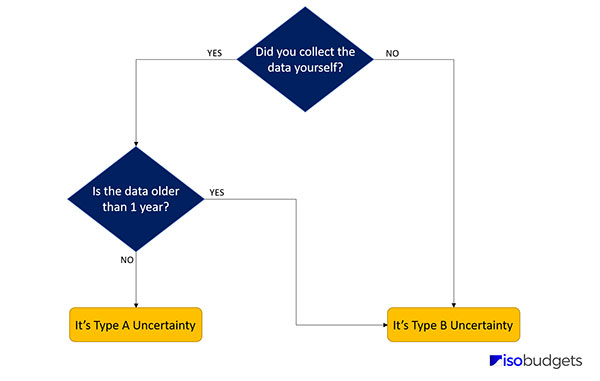
Probability Distributions
This is an important step because the probability distribution that you select will determine how your source of uncertainty is converted to a standard deviation in the next step.
Although there are many different types of probability distributions that you can choose from, the Normal (i.e. Gaussian) and Rectangular (i.e. Uniform) distributions are the most commonly used.
Probability Distributions for Estimating Uncertainty
Some of the most common probability distributions used to estimate uncertainty are;
- Normal (i.e. Gaussian) Distribution
- Rectangular (i.e. Uniform) Distribution
- Triangular Distribution
- Log-Normal Distribution
- Quadratic Distribution
- U-shaped Distribution
- Rayleigh Distribution
Use the chart below to help you select the appropriate probability distribution.
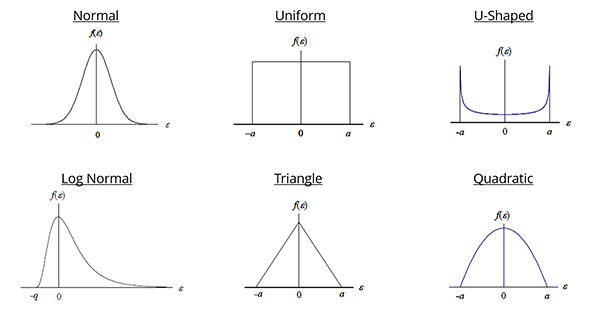
To assign the appropriate distribution, consider how to characterize the data set for each source of uncertainty.
If you evaluated Type A uncertainty data, calibration results, or used an accuracy specification, you most likely want to assign a Normal distribution.
If you evaluated resolution, environmental or physical influences, you may want to use a rectangular distribution.
If you are not sure what distribution you should use, then it is typically less risk to assign a rectangular distribution.
How to Assign a Probability Distribution
When selecting a probability distribution, you have two options to help you find the right one.
- Option A: Create and Evaluate a Histogram
- Option B: Use the Probability Distribution Decision Tree
You will most likely want to use option B.
Option A: Create and Evaluate a Histogram
This option is best for evaluating Type A data, but it more difficult and time-consuming if you do not have statistical software. Most likely, you will not use this method. However, if you do, you will find the instructions below.
To find the find probability distribution, follow the instructions below:
- Create a histogram from your data set.
- Evaluate the histogram.
- Find the probability distribution that best characterizes the data set.
Option B: Probability Distribution Decision Tree
Creating histograms is not for everyone and you can only do it if you have the data. In most cases, you will not have the data needed to create a histogram because many of your uncertainty components will be quantified by information that you find published in manuals, papers, guides, etc.
Therefore, you will need to make some assumptions to select the right probability distribution. To help you out, I created the probability distribution decision tree. It is the best option for Type B data.
If you do not want to or cannot create a histogram of your data set, then try using the probability distribution decision tree. All you need to do is answer the questions below:
1. Did you collect the data yourself via testing and experimentation?
- If YES, choose Normal.
- If NO, go to question 2.
2. Did others (e.g. manufacture, other lab, etc.) collect the data via testing and experimentation?
- If you think YES, choose Normal.
- If NO, go to question 3.
3. Are you not sure how the data was collected?
- If YES (i.e. if you are not sure), choose Rectangular.
- Or, consider question 4.
4. Are the results expected to occur at the extremes of the range?
- If YES, choose U-Shaped.
- If NO, go to question 5.
5. Are the results expected to occur at the center of the range?
- If YES, choose Normal or Triangle.
- If NO, choose Rectangular.
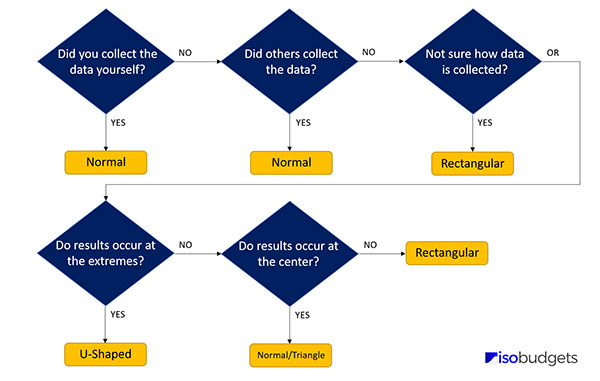
If you want to learn more about probability distributions, check out the following guide:
Step 5: Convert Uncertainty Components to Standard Deviation Equivalents
Once you select a probability distribution, you can identify the equation needed to convert each uncertainty contributor to a standard deviation equivalent. This will reduce each source of uncertainty to a 1-sigma level (i.e. 68.27% confidence), so you can properly combine them using the GUM method in the next step.
Make sure to perform this task for each uncertainty contributor that you quantified in step 3.
How to Convert Uncertainty to Standard Deviations
To convert uncertainty components to standard deviations, follow the steps listed below:
- Assign a probability distribution to each source of uncertainty,
- Find the divisor for the selected probability distribution,
- Divide each source of uncertainty by it’s respective divisor.
Refer to the chart below to find the divisor associated with the probability distribution that you selected in step 4.
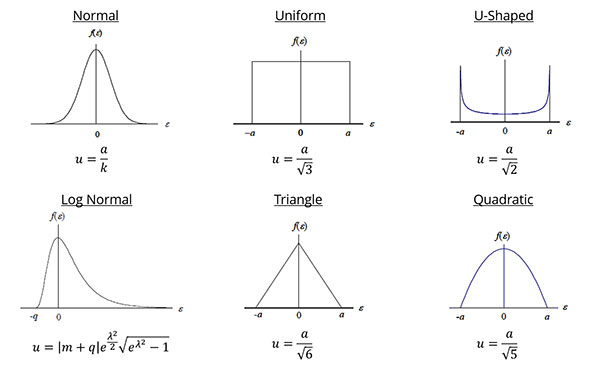
Next, divide your uncertainty components by the appropriate divisor to convert them to a standard uncertainty. Afterward, all of your contributors should be on the same confidence level (i.e. 1-sigma or 68.27%) and equivalent to a standard deviation.
What Divisor to Use to Convert Uncertainty
To convert uncertainty to standard deviations, it is best to understand more about probabilities distributions and their associated divisors.
Normal Distribution
If you select a Normal distribution, then you will divide your uncertainty by it’s associated coverage factor, k.
Use the Table from the JCGM 100:2008, Appendix G.
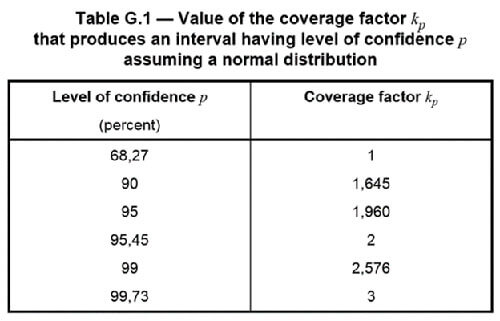
Take a closer look at the sources of uncertainty that you are evaluating to determine what coverage factor you should use. Typically, your contributors will have a confidence level of 68%, 95%, or 99%. Respectively, this means that you will use a divisor of 1, 2, or 2.576.
Rectangular Distribution
If you select a Rectangular distribution, then you will divide your uncertainty component by the square root of 3 or 1.7321.
U-Shaped Distribution
If you select a U-shaped distribution, then you will divide your uncertainty component by the square root of 2 or 1.4142.
Triangular Distribution
If you select a Triangular distribution, then you will divide your uncertainty component by the square root of 6 or 2.4495.
Quadratic Distribution
If you select a Quadratic distribution, then you will divide your uncertainty component by the square root of 5 or 2.2361.
Log-Normal Distribution
If you select a Log-Normal distribution, then you will divide your uncertainty component by 2.3750.
Rayleigh Distribution
If you select a Rayleigh distribution, then you will divide your uncertainty component by 2.4477.
Handling Components With Different Units of Measurement
The most important thing to remember when converting uncertainty to standard deviation equivalents is to make sure all the standard deviations are in the same units of measurement.
This is critical before calculating the combined uncertainty. Otherwise, your estimated uncertainty will not be correct.
You cannot combine uncertainties with different units of measurement (without the use of sensitivity coefficients).
If you have contributors with different units of measurement, you will need to use sensitivity coefficients to convert them to units of measurement that match the measurement result or a term relative to the measurement result (e.g. percent).
This is a mistake many people make when estimating uncertainty of measurement. So, make sure to check for this before you calculate the combined standard uncertainty.

Sensitivity Coefficients
If you want to learn more about sensitivity coefficients, just click the link below to check out my guide on sensitivity coefficients.
Step 6: Calculate the Combined Uncertainty
After converting your uncertainty sources to standard deviation equivalents, it is time to calculate the combined uncertainty using the root sum of squares (i.e. RSS) method recommended in the Guide to the Expression of Uncertainty in Measurement (i.e. GUM; JCGM 100:2008).
This will mathematically combine your uncertainty sources in quadrature. So, keep reading to learn how to combine uncertainty.
How to Calculate the Combined Uncertainty
To calculate the combined standard uncertainty, simply following these instructions:
- Square the value of each uncertainty component,
- Add together all the results in step 1,
- Calculate the square root of the result in step 2.

To summarize the instructions above, simply square the value of each uncertainty source. Next, add them all together to calculate the sum (i.e. the sum of squares). Then, calculate the square-root of the summed value (i.e. the root sum of squares). The result will be your combined standard uncertainty.
After you complete this process, you will have the combined standard uncertainty at a 1-sigma level (i.e. 68.27% confidence) characterized by a Normal distribution per the Central Limit Theorem.
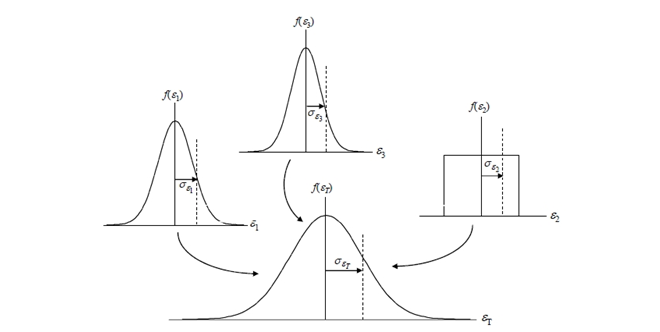
Central Limit Theorem
When you combine uncertainty sources, you are also combining their probability distributions.
According to the Central Limit Theorem, the sum of the set of independent random variables (i.e. uncertainty sources) will approach a normal distribution regardless of the individual variable’s distribution.
Therefore, the probability distribution associated with your combined uncertainty will now be normal. Look at the image above for a visual representation.
Root Sum of Squares Method
If you are a more visual learner, like me, take a look at the process below to see if it makes more sense.
Below, you will see the equation for calculating the combined uncertainty.
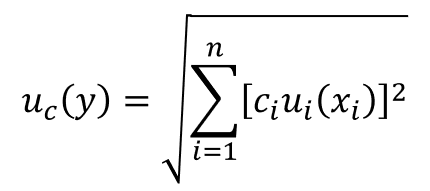
ci = sensitivity coefficient
ui(xi) = uncertainty of x
uc(y) = uncertainty of y
If the equation above looks confusing, you can try the simplified version below.
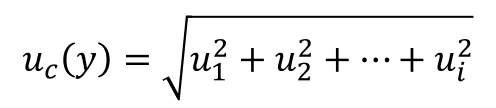
ui = uncertainty of x
uc(y) = uncertainty of y
This is the equation that I typically use since I usually include sensitivity coefficients (i.e. ci) earlier in the process before I convert uncertainty components to standard deviations.
If you evaluate measurement uncertainty the same way, you should be able to use the simplified equation. If you do not use sensitivity coefficients at all, you can use the simplified equation as well.
Both equations give you the same result. So, use the equation that works best for you. If you are using an excel spreadsheet calculator, you may find the function in the next section beneficial.
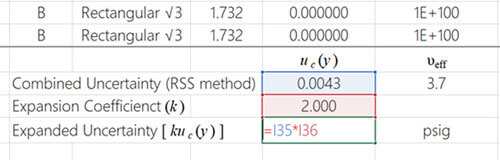
Excel Function for Combining Uncertainty
If you use Microsoft Excel to estimate uncertainty, you can easily combine uncertainty using the formula below. It is a combination of the square root and sum of squares function.
Take a look at the image below to see the function used in my Simple Uncertainty Calculator.

If you want to learn more about calculating the combined uncertainty, click the link to read the guide:
Step 7. Calculate the Expanded Uncertainty
You are almost done estimating uncertainty, so stay with me. I am going to show you how to calculate expanded uncertainty.
In this step, you are going to learn how to calculate the expanded uncertainty to a 95% confidence interval. To do this, you will need to select a coverage factor and multiply it by the calculated combined uncertainty.
Look at the image below to see the normal probability distribution when you expand your uncertainty to 2-sigma or 95.45% confidence.
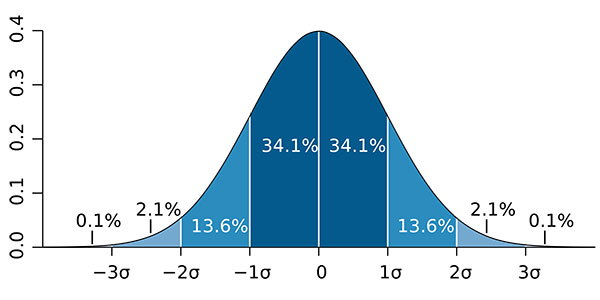
How to Calculate the Expanded Uncertainty
To calculate the expanded measurement uncertainty, just follow these steps:
- Calculate the Combined Uncertainty,
- Calculate the Effective Degrees of Freedom (optional),
- Find/Select a coverage factor (k), and
- Multiply the combined uncertainty by the coverage factor.
The result will be the expanded uncertainty and if you use a coverage factor of 2 or 1.96, you will expand uncertainty to a 95% confidence level.
Check out the simplified equation below for calculating the expanded uncertainty.
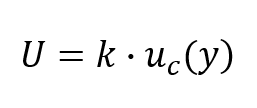
EU – Expanded Uncertainty
k – Coverage Factor
CU – Combined Uncertainty
In the next section, you will learn some options for selecting a coverage factor.
Selecting a Coverage Factor
The coverage factor is the multiplier that you will use to expand uncertainty to a 95% confidence interval. However, you have some options. You can use:
- k=2 for a 95.45% confidence interval,
- k=1.96 for a 95% confidence interval, or
- the Student’s T table to find your coverage factor (k).
Click the link below to see the Student’s T table.
Coverage Factors and Expanded Uncertainty
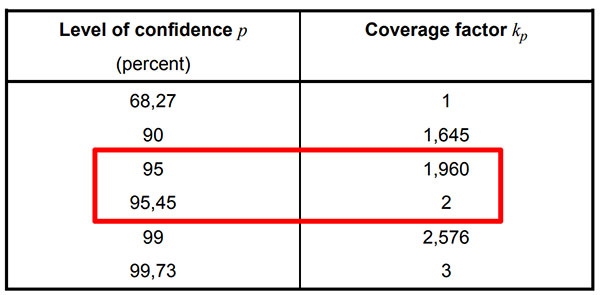
To meet ISO/IEC 17025:2017 requirements, you must expand uncertainty to approximately 95%. Most people use an expansion factor (k) of 2 to achieve a confidence interval of 95.45%. However, you can also use an expansion factor of 1.96 for a confidence interval of exactly 95.00%.
Additionally, you can find your coverage factor using the Student’s T table. This is not common, but it is an option if you need it. Just calculate the effective degrees of freedom using the Welch Satterthwaite equation and use the table to find the right coverage factor to achieve a 95% confidence interval.
The choice is yours. Just make sure to select an expansion factor that you will consistently use in each of your uncertainty analyses. Furthermore, it helps to know why you chose your expansion factor so you can justify it to assessors (if they ask).
- Use a standard k-factor (e.g. 2 or 1.96) when your uncertainty budget contains plenty of sources of uncertainty (Type A and Type B) each with their own value,
- Use the Student’s T table when your uncertainty analysis is limited to mostly Type A data and it is difficult to find or quantify other sources of uncertainty.
Calculating the Expanded Uncertainty
After finding your coverage factor (k), calculate the expanded uncertainty by multiplying the coverage factor and the combined standard uncertainty. Use the formula below for guidance.
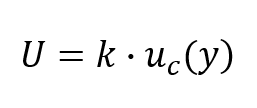
The result is the expanded uncertainty (i.e. U). This is your uncertainty in measurement estimated to a 95% confidence interval.
Look at the image below to see the equation used in one of my uncertainty calculators.
That’s it! You have just learned how to calculate expanded uncertainty in 7 steps and completed the process for the estimation of uncertainty in measurement.
However, you are not done yet. I recommend that you verify your calculations and evaluate your results. In the next section, I will tell you how to evaluate uncertainty calculations for appropriateness.
To learn more about coverage factors and expanded uncertainty or making CMC Uncertainty equations for your scope of accreditation, click the links below:
Step 8. Evaluate Uncertainty for Appropriateness
Once you have calculated the expanded uncertainty, it is best to evaluate your uncertainty estimate for appropriateness. Essentially, you want to make sure that your measurement uncertainty estimate adequately represents your measurement process and is not overestimated or underestimated.
How to Evaluate Your Uncertainty Budget
To evaluate your expanded measurement uncertainty estimates, use one or more of the following methods listed below. Then, determine if your expanded uncertainty is reasonable and appropriate.
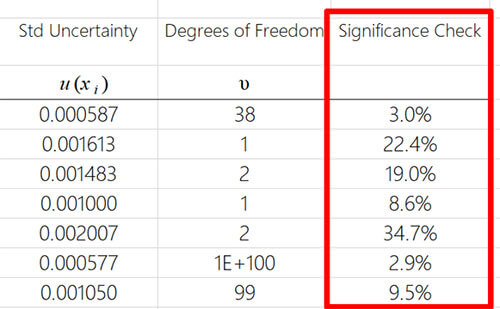
1. Evaluate the Significance of Uncertainty Contributors
For this evaluation, calculate the significance of each source of uncertainty and analyze how much it influences your total measurement uncertainty. Double-check uncertainty components with excessively large and small percentages to verify their value is correct.
2. Expanded Uncertainty vs Reference Standard Uncertainty
For this evaluation, review your expanded uncertainty and verify that it is larger than your Reference Standard Uncertainty. If not, you have a problem and need to double-check the value entered in your uncertainty budget and formulas used to calculate uncertainty.
3. Expanded Uncertainty vs BIPM KCDB
For this evaluation, check the BIPM Key Comparison Database and make sure your expanded uncertainty is larger than the value reported by your national metrology institute (NMI). Sometimes this is not available, but you should at least check.
4. Expanded Uncertainty vs SRM Certificate of Analysis
For this evaluation, review the Certificate of Analysis for the standard reference material that your reference standard is traceable to and verify your uncertainty is larger than the uncertainty of the SRM.
5. Expanded Uncertainty vs Other Labs (Option A
In this evaluation, compare your estimated uncertainty with other laboratories. Search your accreditation body’s database and look at 3 to 5 other laboratory scopes of accreditation to make sure that your expanded uncertainty is reasonably comparable. If not, you may have overestimated or underestimated uncertainty.
This option works best for calibration laboratories since their uncertainty published in their scopes of accreditation. This option is more difficult if you are a test lab. Most test labs do not report their test uncertainties in their scope of accreditation which makes it difficult to compare your capabilities with other laboratories.
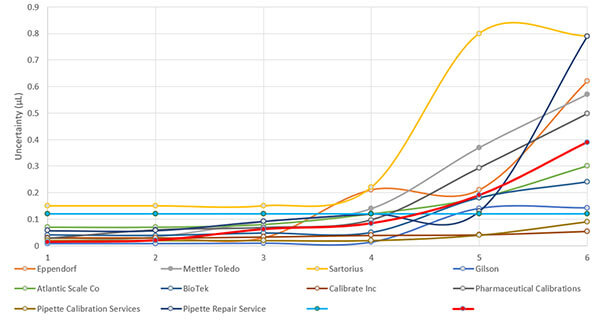
6. Expanded Uncertainty vs Other Labs (Option B)
For this evaluation, participate in a proficiency testing scheme and compare your uncertainty with other laboratories. Then, determine whether or not your results are reasonable and appropriate. Make sure that your expanded uncertainty is not significantly larger or smaller than other participating laboratories.
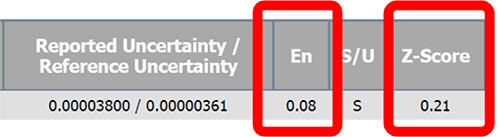
When evaluating your proficiency test results, you really want to look at your z-score more than the normalized error (En) value. Both can be beneficial, but the z-score compares your laboratory’s performance with other participating labs.
If your En score is large or close to the value of one, then you may have reported an understated value of uncertainty or you may have a problem with your measurement process.
If your z-score is large or close to the value of two, then you may have reported an understated value of uncertainty. As a result, you need to evaluate your uncertainty budgets.
7. Expanded Uncertainty vs Type A Data
For this evaluation, perform a Repeatability and Reproducibility study in your laboratory. Verify that your results are not larger than your uncertainty estimation. If so, you may have understated your expanded uncertainty.
Evaluating your uncertainty budgets are critical. Although it is not a fool-proof process, it is better than doing nothing. You do not want to go through all the work of calculating measurement uncertainty only find mistakes during an assessment. It is better to perform the hard work upfront than deal with all the paperwork and headaches that result from being cited a deficiency. Furthermore, evaluating your uncertainty analyses gives you objective evidence to support your results should an assessor question your expanded uncertainty.
I hope that the evaluations given in the section help you validate your results.
Conclusion
Estimating measurement uncertainty is not easy. It requires a lot of time and effort. However, with the right processes, information sources, and tools, uncertainty analysis does not have to be difficult.
In this guide, I have laid out seven steps to help you calculate measurement uncertainty. While this is not a complete how-to guide, I have given you plenty of information to help you perform uncertainty estimation yourself. So, start estimating uncertainty and tell me what works for you and what you struggle with.
If you have additional questions or suggestions that will help improve this guide, contact me and share your comments. I will glad to get your feedback.
If you need more help, please check out some of my uncertainty calculators and measurement uncertainty training classes.
References
Castrup, H. (2007). Distributions for Uncertainty Analysis. Bakersfield, CA: Integrated Sciences Group.
Miller, V. (2002). NISTIR 6919: Recommended Guide for Determining and Reporting Uncertainties for Balances and Scales. Gaithersburg: National Institute of Standards and Technology.
United Kingdom Accreditation Service. (2012). M3003: The Expression of Uncertainty and Confidence in Measurement. Middlesex: United Kingdom Accreditation Service.
JCGM/WG1. (2008). JCGM 100:2008 – Evaluation of measurement data – Guide to the expression of uncertainty in measurement. Sèvres: BIPM.






13 Comments