Calculating normalized error is common for laboratories participating in proficiency testing or interlaboratory comparisons. If you have participated in a proficiency test before, you may have noticed it in your final summary report either by name or abbreviated ‘En.’
When you participate in proficiency tests, the PT provider calculates normalized error for you. However, if you are participating in interlaboratory comparisons because there is not a proficiency test available, you may have wanted to know how to calculate normalized error to analyze your test results.
In this article, I am going to explain what normalized error is and how to calculate it. After reading this article, you should be able to calculate normalized error long-hand, using a calculator, and(or) using MS Excel.
What is Normalized Error
Normalized error is a statistical evaluation used to compare proficiency testing results where the uncertainty in the measurement result is included. Typically, it is the first evaluation used to determine conformance or nonconformance (i.e. Pass/Fail) in proficiency testing.
Normalized error is also used to identify outliers in the proficiency test results. Sometimes, outliers are removed from the calculations of adjusted mean to prevent influence of excessive offsets.
Why Normalized Error is Important
Proficiency testing is a requirement of ISO17025. If your laboratory needs to performed proficiency testing but is unable to find a PT provider, you may need to perform an interlaboratory comparison. Using the normalized error equation will allow you to evaluate the results in a manner that is acceptable to your accreditation body.
How to Calculate Normalized Error
To calculate normalized error (i.e. En), use the formula below as a reference. If you need some help, keep reading; I am going to walk you through the calculation process.
1. First, calculate the difference of the measurement results by subtracting the reference laboratory’s result from the participating laboratory’s result.
2. Next, calculate the root sum of squares for both laboratories’ reported estimate of measurement uncertainty.
3. Finally, use the value calculated in the first step (i.e. difference of measurement results) and divide it by the value calculated in the second step (i.e. RSS of Uncertainties).
If your results are satisfactory, the value of En should be between -1 and +1. If not, you may have a problem with your measurement process.

Example Normalized Error Calculation
Need an example? I am going to calculate normalized error using data from one of my proficiency tests. In the proficiency test, I compared my Fluke 732A DC Reference Standard to a Fluke 732B sent to me by NAPT.
Looking at the test data, you can see that my Fluke 732A had a value of 9.9999361V with an uncertainty of 0.000028 V (i.e. 2.8ppm) and the Fluke 732B had a reference value of 9.99993365 with an uncertainty of 0.00000044V (i.e. 0.044 ppm). After calculating normalized error, or En, the result yielded a value of 0.09 which is between -1 and +1. So, my results were satisfactory.
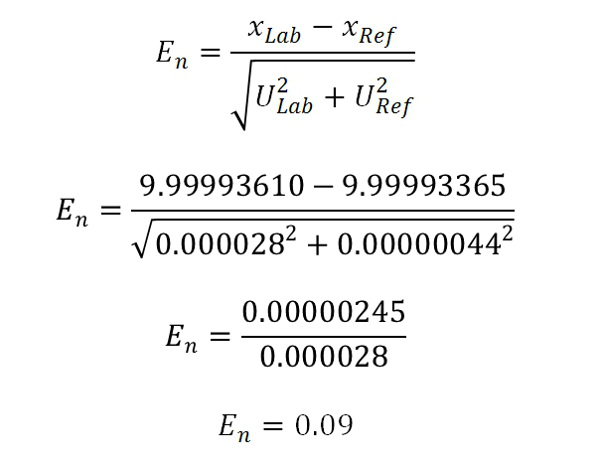
Calculate Normalized Error using Excel
Instead of calculating normalized error the long way, try using MS Excel. It is fast and easy to build a spreadsheet calculator where you can perform multiple calculations very quickly. To make life easy, use the image and equation below as a guide.
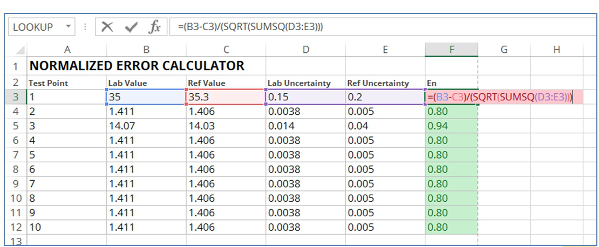
After you have completed the first line of data with the equation, simply copy and paste cell F3 down column F for as many calculations as you need. Using MS Excel is the fastest way to calculate normalized error for your interlaboratory comparisons.
Evaluating Normalized Error
Evaluating the results of the normalized error equation is pretty easy. Calculated values between -1 and +1 are considered conforming or passing. Results outside of this range are considered nonconforming or failing.
Conclusion
Calculating normalized error is not common unless you are a proficiency testing provider. However, if you do not have a proficiency testing provider and(or) participate in interlaboratory comparisons, you may need to know how to calculate normalized error. Even if you have a proficiency testing provider, sometimes it is best to double check their calculations. I have found some mistakes over the years which changed my test results from failing to passing.





13 Comments