Introduction
Expanded uncertainty and coverage factors are an important part of calculating uncertainty. Calculating them is not very difficult, but coverage factors can be a little confusing.
To prevent you from using the wrong coverage factor to calculate expanded uncertainty, I have prepared this article to show you how to find the right coverage factor for you and calculate expanded uncertainty.
Background
When I started calculating uncertainty, I followed the recommendation of assessors to use a coverage factor of 95% where k=2. However, while I was in graduate school taking “Statistics for Quality Control” I realized a 95% confidence interval really has a k factor equal to 1.96, not 2.
So, I spent some time using the Student’s T table and calculating uncertainty using Bayesian Statistics. After using the Student’s T table, I found that a coverage factor where k=2 was really 95.45%.
I also realized that a coverage factor where k=3 was not equal to a 99% confidence interval. Instead, I found that it is equal to a 99.73% confidence interval. This is hardly equivalent to 99%. Again using the Student’s T table, I found that I should be using a coverage factor where k=2.58 if I wanted a 99% confidence interval.
Rather than just use recommended coverage factors, I decided to start using the appropriate coverage factors to achieve 95% and 99% confidence intervals. To further support the use of these coverage factors, I read through the Guide to the Expression of Uncertainty in Measurement (GUM).
The result, my ISO/IEC 17025 assessors accepted my uncertainty estimates using these coverage factors.
Later on, I began to get tired of using the Student’s T table every time I performed an uncertainty analysis. I wanted to find a way to identify my coverage factors quickly. So, I started exploring MS Excel functions to help speed up the process.
After a little research, I came across the “TINV” function and I have been using it ever since. The “TINV” function has helped me automate finding my coverage factors when calculating uncertainty in MS Excel.
To help you out, I am going to share this information with you so you can quickly find coverage factors and calculate expanded uncertainty.
Why is it Important
The goal of calculating expanded uncertainty is to establish a confidence interval where your measurement results have a likelihood of occurring. To accomplish this, you need to know 2 things:
1. How much confidence do you want?
2. What is your calculated combined uncertainty?
So, the first question aims to establish how confident do you want your measurement results to be. Typically, most industries either aim for 90%, 95%, or 99% confidence. What this means is you want your measurement results to occur within a range of values 90%, 95%, or 99% of the time.
With a 90% confidence interval, you want 90 measurement results out of 100 to be within the limits of your uncertainty estimates. It also means that you are accepting a 1 in 10 failure rate. That is right. 1 measurement result out of every 10 is likely to fail and occur outside the bounds of your confidence interval.
With a 95% confidence interval, you want 95 measurement results out of 100 to be within the limits of your uncertainty estimates. At 95% confidence, you are accepting a 1 in 20 failure rate.
With a 99% confidence interval, you want 99 measurement results out of 100 to be within the limits of your uncertainty estimates. At 99% confidence, you are accepting a 1 in 100 failure rate.
The second question aims to notify you that you need to know your combined uncertainty in order to calculate expanded uncertainty. If you do not know how to calculate combined uncertainty, you should probably read this article to learn how to calculate combined measurement uncertainty.
Expanded Uncertainty
Expanded uncertainty is the last calculation when estimating uncertainty in measurement. Typically, it is very easy and only requires you to multiply the combined uncertainty by a desired coverage factor.
However, before I jump into how to calculate expanded uncertainty, let’s learn a little more about it.
The best place to start is by defining expanded uncertainty. So, below I have given you the definition of expanded uncertainty from the 2012 edition of the Vocabulary in Metrology.
Definition
2.35 Expanded Measurement Uncertainty (Expanded Uncertainty)
product of a combined standard measurement uncertainty and a factor larger than the number one
NOTE 1 The factor depends upon the type of probability distribution of the output quantity in a measurement model and on the selected coverage probability.
NOTE 2 The term “factor” in this definition refers to a coverage factor.
NOTE 3 Expanded measurement uncertainty is termed “overall uncertainty” in paragraph 5 of Recommendation INC-1 (1980) (see the GUM) and simply “uncertainty” in IEC documents.
The definition of expanded uncertainty is pretty straight forward and pretty much explains how to calculate it too. Therefore, the next thing I will teach you about expanded uncertainty is the equation you will need to calculate it.
Equation
The equation for calculating expanded uncertainty is very basic. To calculate expanded uncertainty (U), you will need to multiply a coverage factor (k) by the combined uncertainty ( uc(y) ).
To get a visual perspective, I have provided the expanded uncertainty equation for you below.
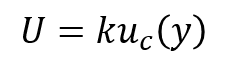
Where,
U = expanded uncertainty
k = coverage factor
uc(y) = combined uncertainty
Now I know that we have already covered how to calculate expanded uncertainty, but writing out the procedure step by step sometimes helps you better understand the process.
So, follow the steps below to calculate expanded uncertainty.
How to Calculate
1. Calculate the Combined Uncertainty.
2. Determine the Coverage Factor.
3. Multiply the Cover Factor and the Combine Uncertainty
Next, let’s look at an example of calculating expanded uncertainty. Below, I have given you a very general example of a scenario to calculate expanded uncertainty. It should help you better understand the process.
Example
Imagine you are estimating uncertainty for the calibration of a Multimeter measuring 10 VDC. After combining your uncertainty sources, your calculated combined uncertainty is 0.0010 VDC.
Now, you want to expand your uncertainty to meet a 95.45% confidence where k=2.
Just multiply the combined uncertainty by the coverage factor.
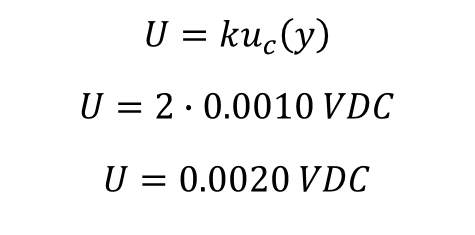
Coverage Factors
Coverage factors are important when calculating uncertainty. However, most of you probably just choose a 95% confidence interval and use k=2. Am I Right?
Well, have you ever stopped to think about why we use k=2 or how much confidence a value of 2 gives you?
What if I told you that k=2 is really equal to a confidence interval of 95.45%, not 95%. If you really want to establish a confidence interval of 95%, you should use a coverage factor where k=1.96.
Furthermore, you probably thought that a 99% confidence interval was equal to a coverage factor where k=3. Well, not really! A confidence interval of 99% is actually equal to a coverage factor where k=2.58, and a coverage factor where k=3 is really equal to a confidence interval of 99.73%.
If this surprises you, stop listening to what others have been telling you and keep reading. I am about teach you everything that you need to know about coverage factors. After reading this, you should be able to find appropriate coverage factors for you, be able explain how you calculated them, and why you use them.
It is all really simple statistics. Also, the best part is you can always fact-check your methods and calculations with scholarly sources from university websites. Some of my favorite university websites for statistics are:
What Coverage Factor Should You Use
Coverage factors are typically a recommendation based on industry consensus and best practices. If you are a student, you most likely estimate uncertainty to a confidence interval of 68.27% where k=1.
If you are the metrology industry and seeking ISO/IEC 17025 accreditation, you typically estimate uncertainty to 95.45% confidence and use a coverage factor where k=2.
If you are in the manufacturing industry, you are most likely aiming for a failure rate of 1 in 10,000 or a coverage factor of 99.99% confidence, where k=3.89. However, the manufacturing industry varies, so confidence intervals can be greater or smaller depending on acceptable failure rates.
Definition
2.38 Coverage Factor
number larger than one by which a combined standard measurement uncertainty is multiplied to obtain an expanded measurement uncertainty
NOTE A coverage factor is usually symbolized k (see also ISO/IEC Guide 98-3:2008, 2.3.6).
The definition of coverage factor from the Vocabulary in Metrology even relates to the calculation of expanded uncertainty. Therefore, you now understand why I combined these two topics in this article.
Next, I am going to show you how to calculate your coverage factor the easy way.
Equation
The equation below is the function that you will use to calculate your coverage factor in MS Excel. Now, I could have given you the Student’s T distribution function. However, I do think the majority of you reading this would want to use the actual equation. So, I have omitted it from this article.
=TINV(probability, degrees of freedom)
To find the probability:
Probability = (1-α) = (1-0.95) = 0.05
Find the Degrees of Freedom
Degrees of Freedom = n-1
How to Calculate
Method 1
1. Calculate the Effective Degrees of Freedom.
2. Refer to the Student’s T Table.
3. Find the Column that matches your confidence interval or probability.
4. Find the row matching your degrees of freedom.
5. Find the value where your column and row meet.
This is your coverage factor for k.
Method 2
1. Open a new MS Excel workbook.
2. Select a cell and type in the “TINV” function.
3. Enter your probability value and your degrees of freedom.
4. Hit Enter and find your coverage factor.
Calculating your coverage factor is not difficult, but there are a few steps that you will need to perform to find it. For the majority of you calculating uncertainty, just use coverage factors with an infinite degrees of freedom. It will make calculating uncertainty easier for you.
If using the MS Excel function above, use the number 1,000,000 or 1E+06 for infinite degrees of freedom. If you are using the Student’s T table instead of the MS Excel function, just look at the values at the bottom of the table (usually the last row). It will marked with the infinity symbol.
You can use this coverage factor for all of your uncertainty calculations. It will make calculating uncertainty faster and easier, and will not have to calculate a coverage factor each time you estimate uncertainty.
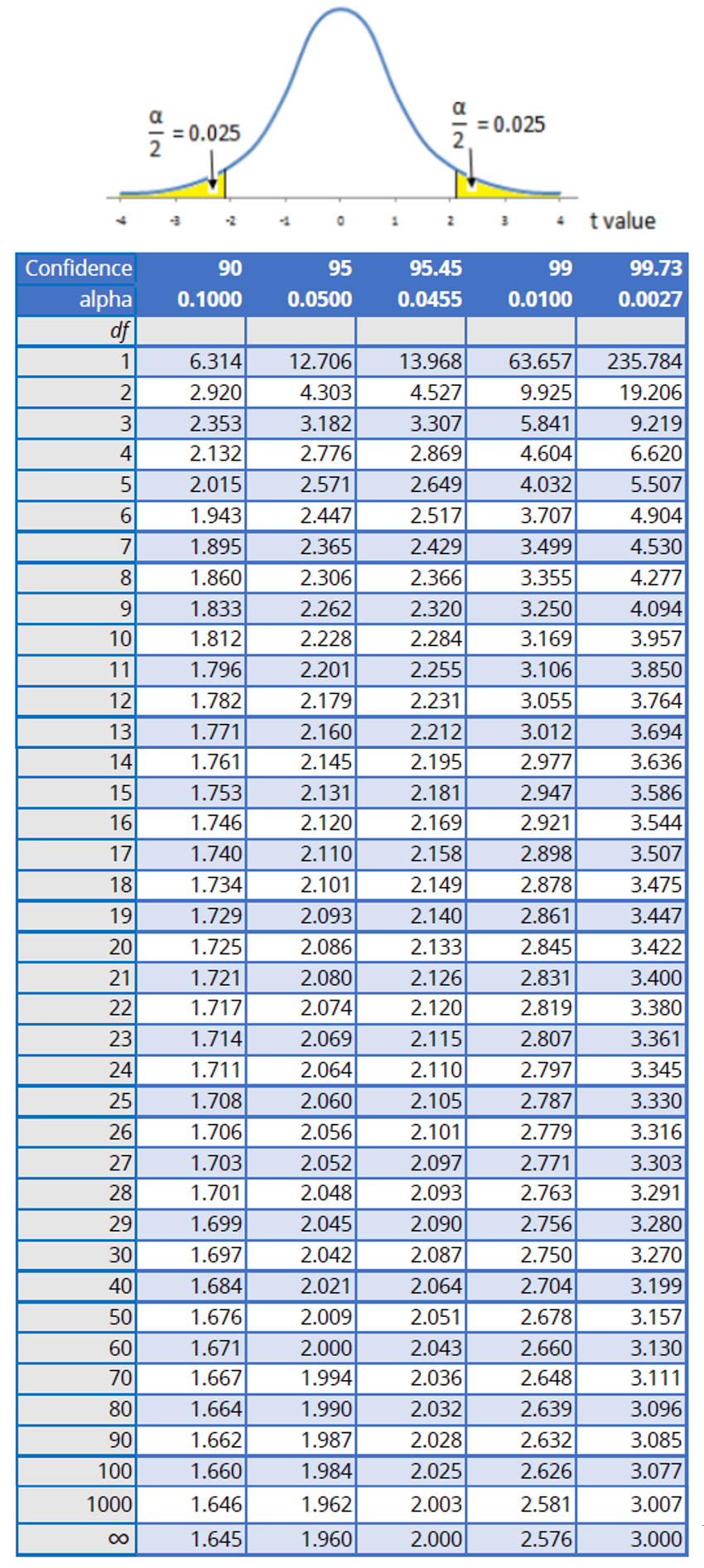
To help you out, I have created a custom Student’s T table. Unlike most of the Student’s T tables on the internet or in statistics textbooks, the chart that I created is specially made for the Metrology industry.
The table below has coverage factors for 90%, 95%, 95.45%, 99%, and 99.73% confidence intervals, so you can choose to use k-factors of 1.96, 2.00, 2.58, and 3.00.
If you are still confused about calculating coverage factors, let’s look at an example scenario that I prepared to showcase how to find coverage factors.
Example
Imagine that you have just calculated the combined uncertainty for your uncertainty analysis and calculated the effective degrees of freedom using the Welch-Satterthwaite equation.
You find that you have 19 degrees of freedom and you want to find the coverage factor for 95% confidence.
Looking at the Student’s T table, find the column for 95% confidence.

Now, find the row that matches your degrees of freedom.
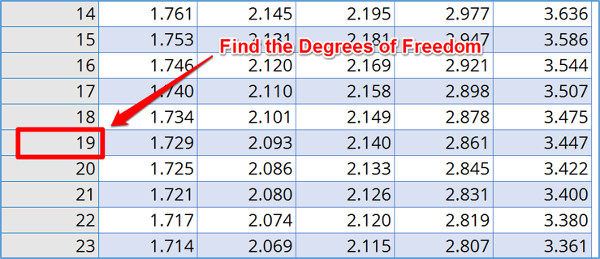
Where the column and row meet, you will find your coverage factor.

From the Student’s T table, the coverage factor is k=2.093.
If you don’t have a Student’s T table lying around, don’t have an internet connection, or just don’t feel like looking at the table again, open up MS Excel. Now, select a cell and type in the following function;
=TINV(0.05,19)
Next, hit the ‘Enter’ key and Excel will calculate your coverage factor, which should be k=2.093.
If you download my Student’s T Table and coverage factor calculator, first select your desired coverage factor from the drop-down menu.

Next, enter your degrees of freedom.

Then, enter the following MS Excel function. It is already provided in the coverage factor calculator.

Finally, MS Excel will calculate your coverage factor.

Conclusion
Calculating expanded uncertainty and coverage factors are an essential task to estimating uncertainty. It is important that you select the appropriate coverage factor for your uncertainty analysis. So, be sure to use the tools that I have provided for you. It will make the uncertainty estimation process much easier for you.
Now, leave a comment below and tell me what industry you are in and what coverage factor you use.
References
JCGM. (2012). International Vocabulary of Metrology: Basic and General Concepts and Associated Terms. Sèvres: BIPM.





14 Comments