
Test Uncertainty Ratio Definition
Test Uncertainty Ratio or TUR is a common term used in calibration. It is the ratio of the tolerance or specification of the test measurement in relation to the uncertainty in measurement results.
According to the ANSI Z540.3 Handbook, the official definition is the ratio of the span of the tolerance of a measurement quantity subject to calibration, to twice the 95% expanded uncertainty of the measurement process used for calibration.
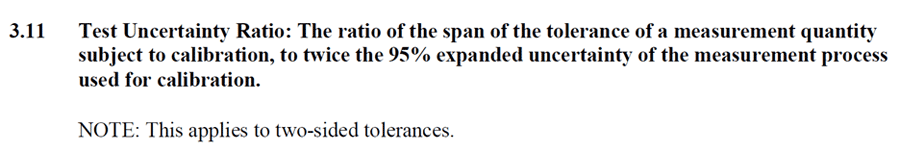
Measurement Capability Index
In some parts of the world, test uncertainty ratio is known as measurement capability index.
According to the JCGM 106:2012, measurement capability index is the tolerance divided by a multiple of the standard measurement uncertainty associated with the measured value of a property of an item.

Essentially, test uncertainty ratio and measurement capability index are the same. Therefore, the information in the rest of this guide will apply equally to measurement capability index.
Purpose of Test Uncertainty Ratio
TUR is used to evaluate measurement risk and validate the use or suitability of calibration methods and measurement systems. The most common cited recommendation for many calibrations is a 4:1 TUR.
However, due to advances in technology, not all calibrations are capable of meeting a 4:1 TUR. When performing evaluations, make sure to compare your TUR calculations to similar measurement systems. Otherwise, you may waste a lot of time and money chasing a TUR value that is not obtainable.
Now that you know the purpose of TUR, let’s learn how to calculate TUR so you can evaluate your measurement capabilities.
Test Uncertainty Ratio Formula
To calculate the Test Uncertainty Ratio, we must know the value of the following:
- tolerance or specification limit; and
- uncertainty in measurement.
Once this information is known, you can use the following equation to calculate TUR.
The TUR Formula
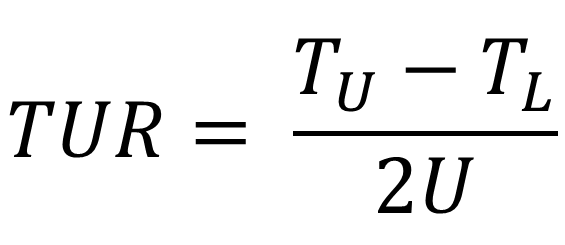
TUR = Test Uncertainty Ratio
TU = Upper Tolerance Limit
TL = Lower Tolerance Limit
U = Expanded Uncertainty
How to Calculate Test Uncertainty Ratio
Now that you have the TUR equation, I am going to teach you how to calculate Test Uncertainty Ratio step by step. Following the instructions below to calculate TUR.
- Specify the measurement parameter,
- Find the tolerance or specification limit(s),
- Calculate the uncertainty in measurement,
- Subtract the upper tolerance limit by the lower tolerance limit,
- Multiply the expanded uncertainty by 2,
- Divide the result of step 4 by the result of step 5, and
- Round the result to 2 significant figures.
In the next section, you will see how to calculate TUR in Microsoft Excel. Plus, there are several test uncertainty ratio examples given below.
Calculate Test Uncertainty Ratio in Excel
Now that you have the TUR formula and know how to calculate it, you may want to calculate your test uncertainty ratio in Microsoft Excel, Crystal Reports, or similar software.
In the image below, you will see how to calculate TUR in Microsoft Excel.
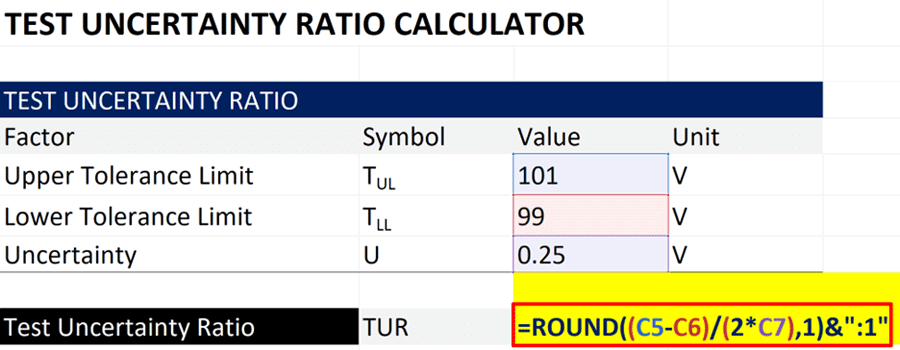
Here is the formula that I used in the image above.
=ROUND((C5-C6)/(2*C7),1)&”:1″
The cells or fields in your formula may differ, but the function is still the same: calculate the difference between the upper and lower tolerances, divide the result by two times the expanded uncertainty, and round the result to one decimal place.
Test Uncertainty Ratio Examples
Calculating TUR can vary based on different tolerance scenarios. In this section, you will learn how to calculate TUR for several common situations. If need more information, you can find many of these scenarios in the ANSI Z540.3 Handbook and the JCGM 106:2012.
The scenarios covered in this section are:
- Symmetrical Tolerances,
- Asymmetrical Tolerances,
- Logarithmic Tolerances,
- Maximum Permissible Error, and
- Single-Sided Tolerances.
TUR for Symmetrical Tolerances
Calculating test uncertainty ratio for symmetrical tolerances is very common. Most tolerance intervals are symmetrical about the nominal or target value.
For symmetrical tolerances, calculate TUR using the formula given below.
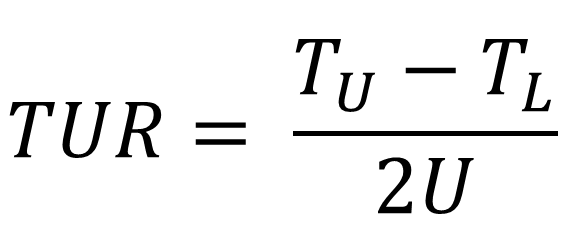
TUR = Test Uncertainty Ratio
TU = Upper Tolerance Limit
TL = Lower Tolerance Limit
U = Expanded Uncertainty
In the image below, you will see the calculation of TUR for a 100 VDC measurement with a tolerance of ±1 VDC (i.e. 1% of reading) and an expanded uncertainty of 0.25 VDC (95% confidence where k=2).
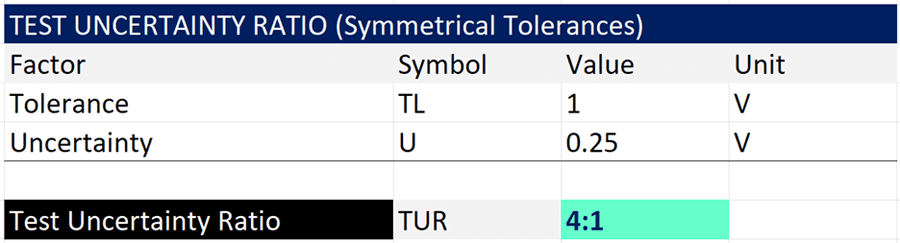
Since the tolerance is symmetrical, you can simply divide the tolerance by the expanded uncertainty to calculate a 4:1 TUR.
TUR for Asymmetrical Tolerances
Occasionally, you will encounter tolerances that are not symmetrical (i.e. the upper and lower tolerances are not equal in magnitude from the target or nominal value). However, you can still calculate the TUR.
For asymmetrical tolerances, calculate test uncertainty ratio using the formula given below.
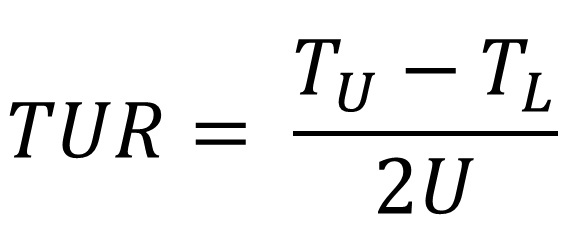
TUR = Test Uncertainty Ratio
TU = Upper Tolerance Limit
TL = Lower Tolerance Limit
U = Expanded Uncertainty
In the image below, you will see the calculation of TUR for a 100 VDC measurement with an upper tolerance limit of 101.1 VDC, a lower tolerance limit of 99 VDC, and an expanded uncertainty of 0.25 VDC (95% confidence where k=2).
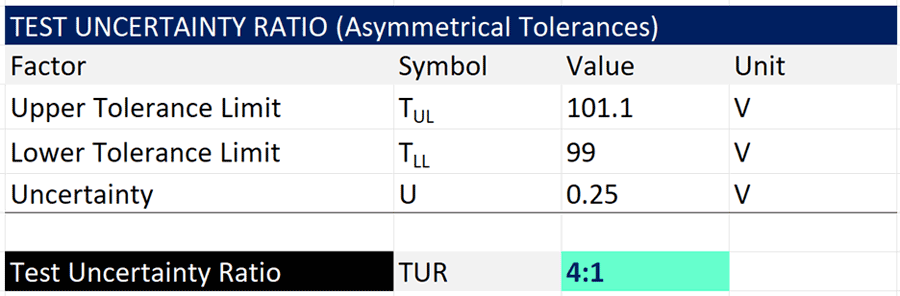
Since the tolerance is asymmetrical, you must first subtract the upper tolerance limit by the lower tolerance limit. Then, divide the result by two times the expanded uncertainty.
The calculation yields a 4:1 TUR.
TUR for Logarithmic Tolerances
Logarithmic tolerances are common for certain types of measurements such as RF Power Level and Sound Power Level.
At first glance, the tolerances may appear to be symmetric. However, they are not.
For logarithmic tolerances, you must first convert the values to linear values. Then, calculate test uncertainty ratio using the formula given below.
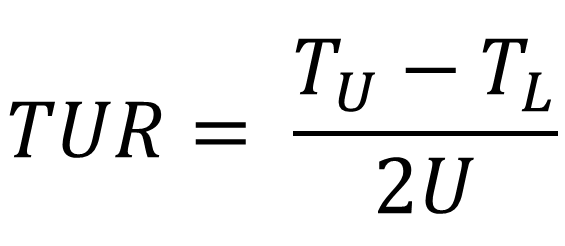
TUR = Test Uncertainty Ratio
TU = Upper Tolerance Limit
TL = Lower Tolerance Limit
U = Expanded Uncertainty
In the image below, you will see the calculation of TUR for a 20 dBm power level with a tolerance of ±1 dBm and an expanded of 0.25 dBm (95% confidence where k=2).
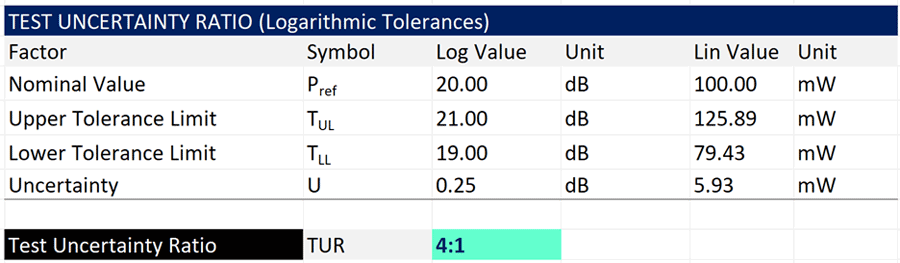
Initially, the upper and lower tolerances seem to be symmetrical. However, when you convert the logarithmic values to linear values, you will notice that the tolerances are not symmetrical.
Since the tolerance is asymmetrical, you must first subtract the upper tolerance limit by the lower tolerance limit. Then, divide the result by two times the expanded uncertainty.
The calculation yields a 4:1 TUR.
TUR for Max Permissible Error
Maximum permissible error (MPE) is a common tolerance given for instruments, such as calibration masses. MPE should be treated as a symmetrical tolerance. Therefore, you will want to use the formula below to calculate the test uncertainty ratio
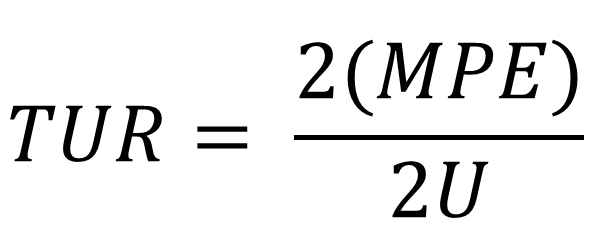
TUR = Test Uncertainty Ratio
MPE = Maximum Permissible Error
U = Expanded Uncertainty
In the image below, you will see the maximum permissible error of a 1 kg ASTM Class 1 weight and an expanded uncertainty of 0.5 mg (95% confidence where k=2).
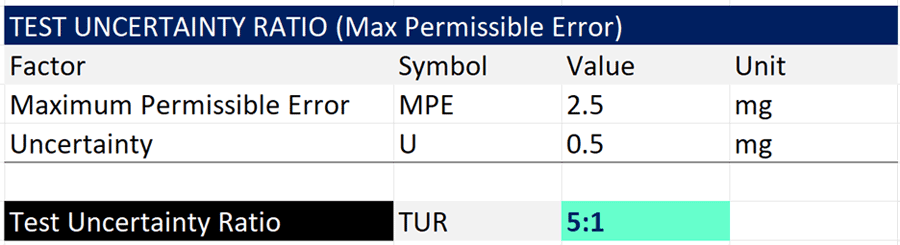
Since the tolerance is symmetrical, you can simply divide the maximum permissible error by the expanded uncertainty to calculate a 4:1 TUR.
TUR for Single-Sided Tolerance
Single-sided tolerances are common. However, standards documents do not provide a solution for calculating TUR. In fact, the ANSI Z540.3 Handbook states that the test uncertainty ratio formula only applies to two-sided tolerances.
This causes a problem, and I receive a lot of questions from people asking how to calculate TUR for single sided tolerances.
Technically, there does not appear to be an official solution. To date, I have not found one.
However, I would recommend using the formula below as an interim solution.
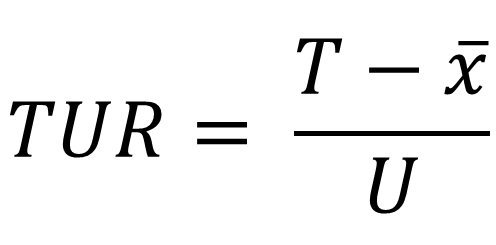
TUR = Test Uncertainty Ratio
TU = Upper Tolerance Limit
xbar = Mean, Nominal, or Target Value
U = Expanded Uncertainty
Now, this formula assumes that your measurement has a nominal or target value. If it does not, then substitute the nominal or target value with the mean measurement value from a set of repeated measurements.
This method is supported by the following resources linked below.
The first resource is a support article from statistical software, Minitab, where they answer how Minitab calculates % Tolerance with a one-sided tolerance.
The second resource is a conference paper on measurement system analysis for one-sided tolerance.
I recommend calculating the difference between the tolerance limit and the nominal value. Then, dividing the result by the expanded uncertainty.
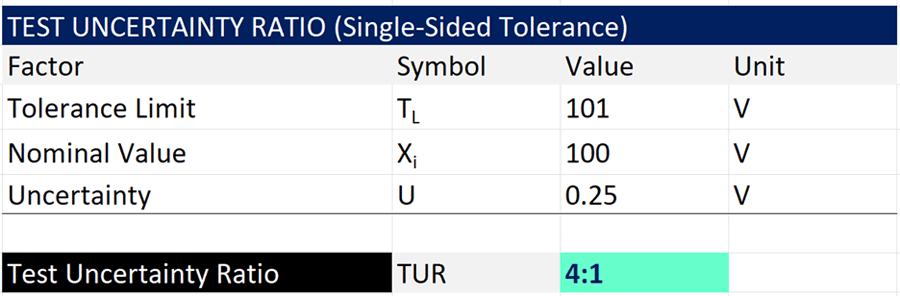
In some cases, the other side of the tolerance may go to infinity. However, I would focus on the interval between the mean or nominal value and the tolerance limit. This will ensure that you evaluate TUR correctly.
Conclusion
Test Uncertainty Ratio is a common metric used to determine the suitability of calibration methods and equipment. Additionally, it is finding new uses for simple acceptance decision rules.
If your TUR is 4:1 or greater, Awesome! You are meeting the general requirements for what most people perceive as a good ratio. If your TUR is less than 4:1, then you may want to evaluate your results further to determine the measurement risk.
Not all measurements or calibrations will meet a 4:1 TUR. It is not possible. Find what is a commonly accepted TUR for your measurement system and compare your test uncertainty ratio to it.
This guide should have covered everything that you need to know about TUR, including:
- What is Test Uncertainty Ratio?
- What is the TUR Formula?
- How to Calculate TUR?
- How to Calculate TUR for Different Tolerance Scenarios?
Now that you have everything that you need, start calculating test uncertainty ratio yourself; or, you can download my TUR Calculator for free by clicking here.
If you are ISO/IEC 17025 accredited with A2LA or UKAS, make sure to read my guide on Simple Acceptance Decision Rules to see how you can use TUR to take uncertainty into account.
——
This article was originally posted on Oct 27, 2014 and updated on 07/17/2023.




15 Comments