How to Calculate Stability for Uncertainty

 
 

Introduction

Stability is an important source of uncertainty. Typically, it is a significant contributor to uncertainty.

As a result, calibration labs should always include the stability or drift of measurement equipment and(or) standards in their uncertainty budgets. Omitting it in an uncertainty analysis will likely result in an understatement of measurement uncertainty (i.e. reporting smaller uncertainty than you should).

For reference, the following documents recommend or require stability (or instability) or drift is included in the uncertainty budget;

1. EA-04/02 M: 2022 – Evaluation of the Uncertainty of Measurement in Calibration,
2. UKAS M3003 – The Expression of Uncertainty and Confidence in Measurement,
3. NIST TN 1297 – Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results,
4. A2LA R205 – Specific Requirements – Calibration Laboratory Accreditation Program,

Additionally, stability or drift is required to be evaluated by many standard methods (e.g. ISO, ASTM, etc) and EURAMET calibration guides.

Since stability is important, I created this guide to teach you all about it including how to calculate the uncertainty.

In this guide, I am going to cover the following information:

 
To jump ahead to any of these sections, click one of the links above. Otherwise, keep scrolling to learn more about stability.

 
 

What is Stability

According to the Vocabulary in Metrology (VIM), stability is a property of a measuring instrument, whereby its metrological properties remain constant in time.

Essentially, it is an evaluation to estimate how much an item’s calibrated or certified value changes over time.

Look at the image below to see the definition of stability in the VIM.

 
If you read the definition notes, you will notice that stability can be calculated several ways.

First, the definition notes state that stability can be based on a time interval that the value or property is expected to change by a specific amount.

Then, it states that stability can be based on a change in the value over a specific time interval.

In either case, you are seeking to determine a change in the metrological property’s value over a specific time interval. Typically, the desired time interval is equal to:

1. one year,
2. the item’s calibration interval, or
3. the item’s period of validity (i.e. until expiration).

Now that you know what stability is, I am going to show you several ways you can calculate stability in the next section.

 
 

How to Calculate Stability

There are several methods you can use to calculate the long-term stability of your standards or measurement systems, including:

1. Stability based on Specifications, Tolerances, or Maximum Permissible Error,
2. Stability based on previous calibration results or control chart data,
3. Stability over a specific time interval,
4. Drift since last calibration, or
5. Average drift over time.

In this guide, I am going to show you how to quantify stability uncertainty using specifications, tolerances, or maximum permissible error, and how to calculate stability using your calibration results or control chart data.

The methods that evaluate drift will be covered in my guide on Drift.

The evaluations in this guide have been sourced from reputable technical documents, standard methods, uncertainty guides, and the consensus opinions of technical experts and assessors.

Most of these methods have been sourced from:

• EURAMET Calibration Guides
• EURACHEM CG4 Uncertainty Guide
• ISO & ASTM Methods,
• OEM Equipment Manuals,
• Measurement Uncertainty Guides, and
• Scholarly Sources (i.e. Textbooks)

 
 

Method 1: Long-Term Stability

 

Description

Long-term stability evaluates how well your measurement equipment’s performance remains constant over time. The evaluation uses your equipment’s historical performance data to calculate stability. You can get this historical performance data from:

1. Equipment calibration reports,
2. Routine intermediate check records, or
3. Control charts.

Once you have the data, calculate the standard deviation of your results to determine the stability of your measurement equipment.

However, make sure the data used in the evaluation is evenly spread over time (i.e. has equal time intervals between the results). Otherwise, your calculated stability will not be accurate.

For example, if you calculate stability using monthly, quarterly, and annual data together, you will get inaccurate results. Therefore, if your data has mixed intervals, then you should calculate average drift over time instead of long-term stability (with a standard deviation).

The average drift over time method takes the different time intervals into account by evaluating the average daily drift rate. As a result, you are less likely to have errors due to uneven time intervals.

Typically, I prefer the average drift method over the long-term stability method. However, the long-term stability method is still a useful evaluation.

The easiest way to determine the stability is to evaluate your measurement equipment’s historical performance data. Most laboratories use the following data to calculate stability:

1. Equipment calibration reports, or
2. Control charts.

Typically, I recommend evaluating performance over the last three to five years. However, you can evaluate more data if you have it.

 
 

Pros and Cons

Calculating long-term stability has its benefits and limitations. Check out the pros and cons of using the method below.

The PROS of this method are:

1. It is easy to evaluate,
2. Takes into account long-term performance trends,
3. Recommended by reputable resources¹.
4. More likely to provide the lab with an accurate CMC uncertainty, and
5. The uncertainty is considered “accurate” not “safe” per JCGM 100:2008, Appendix E

 
The CONS of this method are:

1. Increased risk of overestimating or underestimating uncertainty,
2. Increased risk of false acceptance (i.e. consumers risk),
3. Results can be inaccurate if data has uneven time intervals,
4. Not commonly recommended in reputable methods and uncertainty guides, and
5. May need to update uncertainty budgets more frequently.

 
 

How to Calculate

To calculate long-term stability, follow the instructions provided below:

1. Review the measurement equipment’s last 3 or more calibration/charted results¹,
2. Find the results associated with the value(s) you are evaluating,
3. Record the results from your calibration reports or control charts,
4. Calculate the standard deviation of the calibration results, and
5. Add the standard deviation to your uncertainty budget,
6. Characterize the uncertainty with a Normal distribution where k=1.

 
The calculated stability is a standard deviation. Therefore, you should characterize it with a normal distribution (68% C.I., where k=1). This is important to avoid overestimating or underestimating uncertainty.

 
 

Making Sure Your Process is In Control

Although the long-term stability method is a technically valid evaluation of historic performance, I commonly get opposing feedback from other technical experts that state the method has a high risk of going out of control.

Therefore, I did some research to find an appropriate method of evaluation. Both the NIST SOP-09 and NISTIR 6969 recommend using a t-interval test (similar to a z-score evaluation, but for smaller sample sizes; n < 30) to determine how many standard deviations the results are from the mean.  

The evaluation criteria is as follows:

• |t| > 3: The process is out of control (action required),
• 2 > |t| ≤ 3: Process is in control, but exceeded warning limits (no action required);
• |t| ≤ 2: The process is in control.

Alternatively, ISO 7870-2 provides different evaluation methods and criteria compared to the example above. If you use control charts, I would recommend using the methods in ISO 7870-2. The information in the method is consistent with scholarly resources such as college textbooks on statistical quality control.

 
 

Long-Term Stability Example

In this section, I will show you an example of calculating long-term stability.

Look at the image below. It is a collage of the results from three consecutive calibration reports for the same instrument over time. This will allow me to evaluate the long-term stability of the instrument over this three-year period.

For this example, I am evaluating the long-term stability of a multi-function calibrator to generate a 10 Volt DC output. In the image below, you will notice that I highlighted the results used in my evaluation.

 
Next, I add the results to a stability calculator in Microsoft Excel and use the standard deviation function (i.e. STDEV) to calculate the long-term stability.

In the image below, you will see how I entered the results into the stability calculator. Also, I highlighted the excel function used to calculate stability in the red box on the right-side of the image.

Simply type “=STDEV(”, select the cells that contain the results, type “)”, and hit the Enter key. The function should look similar to the formula given below.

 
Looking at the formula box below, you will find the excel function I used in this evaluation. Copy and paste it into your own spreadsheet calculator. Make sure to replace the values between the parentheses with your own results.

 
Finally, the image below shows the result of the long-term stability calculation. Since the value is a standard deviation, the uncertainty should be characterized with a normal distribution where k=1 (68.27% C.I.).

Knowing this should help you properly evaluate the uncertainty in your uncertainty budget calculator.

 
 

Method 2: Stability Using Specifications, Tolerance, Accuracy, and MPE

 

Description

An easy way to determine stability for your uncertainty analysis is to use manufacturer accuracy specifications, calibration tolerances, or maximum permissible error.

Simply, find these uncertainties by looking at:

1. Equipment manuals and datasheets,
2. Calibration certificates, and(or)
3. Standards documents and methods.

The easiness of the method makes it a popular choice for beginners to estimate uncertainty and labs with customers that do not require results with small uncertainties.

However, this is a conservative method that provides a “Safe” uncertainty because the estimate is considered a deliberate overstatement of uncertainty based on an expected worst case scenario.

To use this method, you need to make the following assumptions about equipment performance:

1. Equipment performance remains within the tolerance interval between calibrations, and
2. Equipment performance is unpredictable between the upper and lower tolerance limits, including at the tolerance limits.

In my opinion, this is a reasonable assumption if you have new equipment with only one calibration report. However, this may not be acceptable for equipment or standards that have an adequate amount calibration history (where trends can be determined and evaluated).

Most standards and equipment are not likely to drift an amount equal to the tolerance. Therefore, using this method could significantly overstate your measurement uncertainty.

According to the JCGM 100:2008, Appendix E, the GUM recommends the use of accurate uncertainties rather than safe uncertainties.

Look at the image below to learn why the GUM recommends “accurate” rather than “safe” uncertainties. Read the following:

1. Section E.1.1,
2. Section E.1.2, and
3. Section E.2.1.

 
Contrary to the GUM, using specifications, tolerances, and(or) MPE is a method highly recommended by manufacturers, accreditation body trainers, assessors, reputable technical guides, and (even) standard methods. Based on consensus, you should be able to use this method to estimate stability without fear of a nonconformity.

I see this technique used all of the time. To date, I have not seen an assessor cite a deficiency (yet) for using this method to evaluate stability or drift. Most likely, they were trained to use this method themselves.

 
 

Pros and Cons

Using specifications, tolerances, and MPE has its benefits and limitations. Check out the below list of pros and cons of using the method.

The PROS of this method are:

1. It’s easy to evaluate,
2. Decreased risk of understating uncertainty, and
3. Update uncertainty budgets less frequently.

The CONS of this method are:

1. The uncertainty is “safe,” not “accurate” per JCGM 100:2008, Appendix E
2. Increased risk of overstating uncertainty,
3. Increased risk of false rejects (i.e. producer’s risk),
4. Lower Test Uncertainty Ratio and Measurement Capability Index, and
5. May impact lab’s ability to meet customer requirements¹.

Overstated uncertainties can impact laboratory performance and the ability to meet customer requirements. The list below provides some of the risks associated with overstated uncertainties.

• Decrease test uncertainty ratio,
• Decrease measurement capability index,
• Incorrect conformity decisions based on the lab’s decision rules,
• Decision rules and the amount of risk taken into account,
• Imbalance between producer and consumer risk.

 
 

How to Find Stability from Specifications, Tolerances, or MPE

To find stability, follow the instructions provided below:

1. Look up the following:
1. Accuracy or uncertainty specifications in manufacturer manuals or datasheets,
2. Stability specifications in manufacturer manuals or datasheets,
3. Tolerance limits in methods or calibration certificates, and(or)
4. Maximum Permissible Error in standards, methods or calibration certificates.
2. Find the value or formula associated with the measurement function, range, and value being evaluated,
3. If the specification is a formula, calculate the uncertainty associated with the value being evaluated. Otherwise, skip this step.
4. Add the specification, tolerance, or maximum permissible error to your uncertainty budget.

 
 

Examples of Stability Based on Specifications, Tolerance, Accuracy, and MPE

In the following sections (below), I am going to show you several examples of using specifications, tolerances, or MPE to evaluate stability.

 
 

Example 1: Accuracy Specification for a Fluke Calibrator

 
The first example I am going to show you is using the manufacturer’s accuracy or uncertainty specifications to calculate stability. In the above image, you will notice that I highlighted the absolute uncertainty specifications with a red rectangle.

If I wanted to use the absolute uncertainty specification (instead of calculating stability), then I would find the formula associated with the value that I above evaluating and calculate the absolute uncertainty associated with the measurand that I am evaluating.

Let’s imagine I need to determine the one-year stability for 329 mV. The formula in the above specifications is 20 ppm + 1 µV. Now, I need to use the formula to calculate my stability uncertainty.

1. First, I set-up the formula as shown in the example below.
2. Next, I multiply the gain coefficient (i.e. slope), 20 ppm, and the measurement value, 329 mV.
3. Then, add the offset coefficient (i.e. y intercept), 1 µV, to the result from the previous step.
4. Finally, round the result to the same number of significant digits as the instrument resolution.

 
The result is the specification that I would use for stability and add to my uncertainty budget.

Additionally, in the above example, take notice that you may have to convert values to make sure they are all the same unit of measure and order of magnitude.

 
 

Example 2: Tolerance of a Gauge Block

 
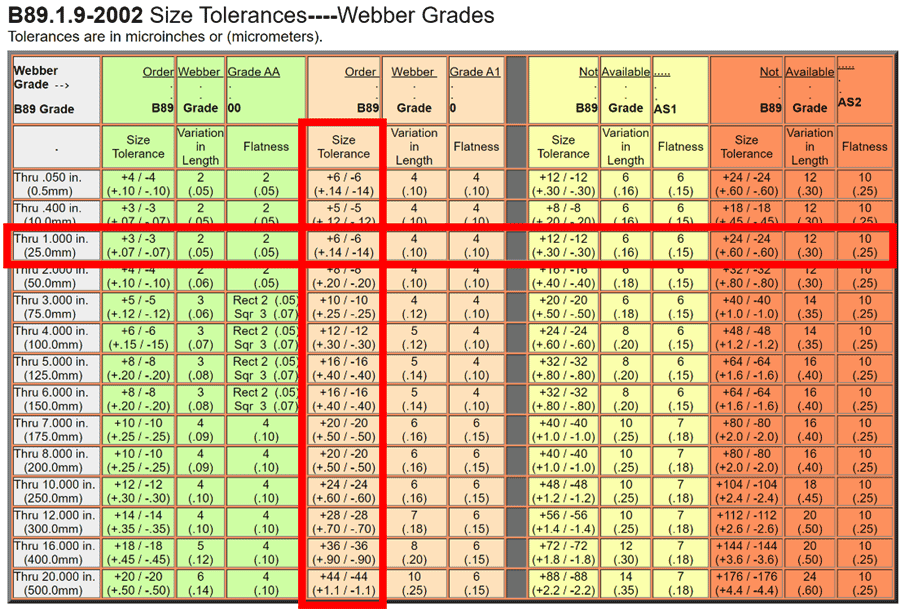
In this example, I am going to estimate stability based on tolerances in the above table. The ASTM B89.1.9, or ISO 3650, is the standard for the metrological characteristics of gage blocks that includes the deviation limits and tolerances based on the size and grade of a gage block.

So, if I know the size and grade of my gage blocks, then I look at the tolerance tables to find stability.

Now, imagine I have a grade 0, one inch gage block. First, I look at the above table and find the Grade 0 column. Next, I look at the rows (on the left side of the table) to find the size range my gauge block is within. Finally, I look at the table to find where the column and row intersect to find the gauge block tolerance.

In this example, the table shows us a grade 0, one inch gage block has a size tolerance of ±6 µin.

This is the value I will add to my uncertainty budget to quantify stability.

 
 

Example 3: Maximum Permissible Error of a Calibrated Mass

 
In this example, I evaluated the stability of a calibrated mass using the maximum permissible error from a tolerance table.

Let’s imagine I have an ASTM Class 1, 100 g mass. To find the maximum permissible error associated with my mass, I performed the following steps:

1. Look up the ANSI/ASTM E617 tolerance tables,
2. At the top of the table, find the column that matches the mass’s assigned class,
3. On the left-hand side of the table, find the row that matches the mass’s assigned value,
4. Find where the column and row intersect to get the mass’s maximum permissible error.

 
The above table shows an ASTM class 1, 100 gram mass has a maximum permissible error of ±0.25 mg.

This value will be used to estimate uncertainty related to the mass’s stability and added to my uncertainty budget.

 
 

Example 4: Tolerance or Maximum Permissible Error of a Calibration Report

 
In this example, I evaluated the stability of a calibrated mass using the maximum permissible error from a calibration certificate.

Let’s imagine I have an ASTM Class 1, 1 g mass. To find the maximum permissible error associated with my mass, I performed the following steps:

1. Look at the most recent calibration report,
2. Find the row that matches the calibrated mass being evaluated,
3. Find the column that contains the mass’s maximum permissible error,
4. Find where the column and row intersect to get the mass’s maximum permissible error.

The above certificate shows an ASTM class 1, 1 gram mass has a maximum permissible error of ±0.034 mg.

This value will be used to estimate uncertainty related to the mass’s stability and added to my uncertainty budget.

If your lab calibrates scales and balances, then this is consistent with Euramet CG-18 and OIML R111. The guides recommend using the mass’s maximum permissible error to evaluate drift (if consecutive calibration results are not available).

 
 

Example 5: Accuracy, Specification, or Tolerances from a Calibration Report

 
In this example, I evaluated the stability of a pressure transducer using the specification/tolerance from a calibration certificate.

Let’s imagine I have a 7MPa pressure transducer and we are evaluating uncertainty at 7MPa (i.e. 7000 kPa in the above image). To find the specification/tolerance associated, I performed the following steps:

1. Look up the item’s most recent calibration certificate,
2. In the report, find the calibration results for the value being evaluated,
3. Find the specification or tolerances (e.g. Upper and Lower Limits).
4. If necessary, evaluate the tolerance as one-half the tolerance interval (see formula below). Otherwise, use the reported specification value.

In the above image, you will see (in the red rectangle) that the calibration report provides the specifications for each test points. Therefore, I can add the specification for 7000 kPa directly to my uncertainty without any additional calculations.

However, most calibration reports do not state the specification. Instead, they report the upper and lower tolerance limits. In this scenario, you will need to use the tolerance limits to calculate the specification before adding it to your uncertainty.

Below, you will see the formula that I recommend using to calculate the specification. You can find this recommendation supported in the JCGM 100:2008 (GUM), sections 4.3.7 and 4.3.8. It works for both symmetrical and asymmetrical tolerance intervals.

Formula

Use the below formula to calculate the stability uncertainty based on upper and lower tolerance limits (typically found in calibration reports).

Where,
U_S – Stability Uncertainty
TL_U – Upper Tolerance Limit
TL_L – Lower Tolerance Limit

 
In the image below, you will see a calibration report that includes the upper and lower tolerance limits. Additionally, you will see the accuracy associated with each test-point listed as well.

With this data, you could use the reported accuracy as the stability uncertainty; or, you could use the tolerance limits and the above formula to calculate the stability uncertainty. The results should be the same as the reported accuracy.

 
After determining the stability uncertainty from either the accuracy, specifications, and(or) tolerances given in a calibration report, I can add it to my uncertainty budget.

 
 

What Method Should You Use

After learning about each of these methods, you may be wondering which one you should use. Well, the answer is the method that you prefer to use and that meets your requirements.

There are so many ways to evaluate data and uncertainty. This makes the task of estimating uncertainty more difficult and confusing (for most people). Additionally, having more options typically causes people to have decision paralysis.

Furthermore, there are so many opinions about what is “best.” This causes so many different recommendations amongst consultants, assessors, and technical experts.

All of the methods in this guide can be found in or supported by the GUM, standard methods (e.g. ISO, ASTM, etc.), or other reputable technical documents (e.g. EURAMET Calibration Guides).

In this section, I am going to cover the pros and cons of each method so you can decide what method is best for you. When deciding which method you will use, take the following into consideration:

1. Laboratory requirements,
2. Customer requirements,
3. Accreditation Body requirements, and
4. The level of risk.

Personally, I use both methods. The method that I choose to use is based on my client’s requirements and the requirements (expectations) of their customers and accreditation body.

In the table below, you will see the pros and cons of each method.

 
TIP: Read JCGM 100:2008, Appendix E.1 and E.2: “Realistic vs Safe uncertainties”

Most assessors and measurement uncertainty training classes recommend using Specifications or Tolerances. It makes estimating uncertainty easier.

However, you are likely to risk encountering an overstatement of uncertainty, including an uncertainty that is larger than the tolerance limit which may significantly impact your lab’s ability to:

1. maintain desired test uncertainty ratios, and(or)
2. meet customer and(or) method requirements.

As a result, you may unnecessarily spend more money purchasing equipment (and calibration services) more accurate than your laboratory needs.

On the other hand, evaluating stability statistically has its own risks. You are likely to understate uncertainty which may significantly impact your laboratory results. You may be able to meet your test uncertainty ratio and customer requirements; however, you may present too much confidence in your results and increase the risk of false acceptance and rejections.

This is a very debatable topic. So, select the method that works best for you and your customers.

 
 

Double Counting Uncertainty

WARNING: Do not overstate your uncertainty.

It is common for people to confuse the terms drift and stability. Many people use terms interchangeably.

First, they are not the same.

Second, do not include both of these factors in your uncertainty budgets (at the same time).

Drift and Stability can confound each other because they evaluate the same set of data using two different techniques.

Make sure to include either Stability or Drift, but not both, in your uncertainty budgets. You are likely to double-count uncertainty components and unintentionally overstate your measurement uncertainty.

In the image below, you will see an excerpt from the JCGM 100:2008 (GUM). Section 4.3.10 offers a warning to not double-count uncertainty components.

 
Please make sure to review your uncertainty budgets are avoid including both drift and stability in the same budget. Only include one of them.

Furthermore, it should be noted (from the above GUM excerpt) that manufacturer specifications typically include contributions due to repeatability, reference standard uncertainty, and(or) resolution. Including these contributors again in your uncertainty budgets is a likely cause of overstating uncertainty.

If the manufacturer publishes specifications for repeatability, reference standard uncertainty, and(or) resolution and states that they are included in the accuracy specification, then consider removing the contribution from the manufacturer specification to avoid overstating measurement uncertainty.

 
 

Conclusion

In this guide you should have learned all about stability and how it affects measurement uncertainty.

I covered the following topics:

1. What is stability,
2. Why stability is important,
3. How to calculate stability,
4. Examples of estimating uncertainty due to stability, and
5. Double-counting uncertainty.

With this information, you should be able to evaluate stability and add the results to your uncertainty budget.

Stability is an important contributor to measurement uncertainty. Sometimes, it is the most significant contributor. So, make sure to evaluate the stability of your measurement equipment and reference standards. Omitting it from your analysis will likely cause you to understate your uncertainty.