
Introduction
Ever wondered what factors are significant contributors to uncertainty in measurement?
Are you performing an uncertainty analysis and wondering what components to include in your uncertainty budget?
Maybe an assessor cited you a deficiency and recommended that you include more sources of uncertainty in your budgets. Afterward, they provided you with a laundry list of significant contributors.
Perhaps, you wanted to reduce your measurement uncertainty by targeting your largest contributors.
If the answer to any of the previous statements was “Yes,” then this guide is for you.
Today, I am going to show you how to find significant contributors by calculating the value of a metric I call “significance.”
Plus, you will learn how to add this calculation to your uncertainty budget in Microsoft Excel, so you automate the calculation every time you estimate uncertainty.
Background
Several years ago, I was at the A2LA Annual Meeting in Maryland discussing measurement uncertainty and significant contributors with a group of technical experts (e.g. metrologists, assessors, and consultants).
One of the topics of conversation was about evaluating uncertainty components to find out how much they contribute to measurement uncertainty.
Dilip Shah, President at E=mc3 Solutions, mentioned a method for determining the amount of influence an uncertainty component contributes to the total uncertainty.
Specifically, I remember him stating that you cannot calculate a ratio of standard deviations. He said that you must convert the standard deviations to variances before calculating the ratios.
Now, I remember learning about this method in college, but never in relation to uncertainty analysis. However, when Dilip mentioned it, I knew that it would be a great tool to evaluate and validate my estimations of measurement uncertainty.
So, I added the calculation to my uncertainty budget templates that night at the hotel. I wanted to test the function to see what I could learn from using it in my uncertainty calculator.
After a few weeks, I realized that it was extremely valuable. It allowed me to quickly;
• find significant contributors,
• find negligible contributors,
• evaluate my results, and
• find errors.
Having this data in my uncertainty budgets helped me validate my results faster. At this point, I couldn’t calculate uncertainty without it.
Therefore, I added it to every uncertainty calculator that I created. Today, I continue to use it and recommend that you give a try.
In this guide, you will learn everything that you need to know about calculating significance and finding significant contributors to measurement uncertainty. I will even show you how to add it your uncertainty budgets.
Here is a list of topics that will be covered in this guide;
1. What is a Significant Contributor
2. What is Significance
3. How to Calculate Significance
4. How to Calculate it in Excel
5. How to Add it to Your Uncertainty Budget
6. How to Validate Your Results
7. Find the Largest Significant Contributors
8. Find the Least Significant Contributors
9. Common Evaluations
What is a Significant Contributor
A significant contributor is a source of uncertainty in measurement that increases the CMC Uncertainty by five percent or more.
According to A2LA, a it is “a contributor whose contribution increases the CMC by five percent (5%) or greater.”
See the excerpt from the A2LA R205 Publication below;
“Significant (A2LA): “significant” further means a contributor whose contribution increases the CMC by five percent (5%) or greater.”
Now, significant contributor is not an official term defined by the Vocabulary in Metrology; but, it is a term used repetitively in several key documents;
• The GUM states, “… significant component to uncertainty of the measurement result.”
• The ISO/IEC 17025:2005 standard states, “… major sources of uncertainty.”
• The ISO/IEC 17025:2017 standard states, “… all contributions that are of significance.”
However, none of these documents define “what is” a significant contributor or establish requirements to determine whether or not a component is a significant contributor to uncertainty.
Therefore, I prefer to refer to the definition provided in the A2LA R205 document. It is the only document to establish requirements for significance.
If laboratories’ uncertainty budgets are going to be assessed for the inclusion of significant contributors, it would be best to rely on requirements rather than opinions.
When a technical expert is allowed to make a decision based on subjective opinions rather than requirements and facts, there will be problems.
Now that you know what a significant contributor is, you may be wondering how to find them in your uncertainty analysis.
Well, it is pretty easy. You just need to calculate a parameter that I call “significance.”
What is Significance
Significance is a proportion, in percentage, of the total uncertainty that a component contributes to the CMC Uncertainty.
While this is not an actual statistical term, it is a term that I have used to describe the magnitude of influence when evaluating significant contributors to uncertainty in measurement.
However, it is statistical method derived from the analysis of variance (ANOVA). Specifically, it is based on the analysis of a proportion of variance or a proportion of total variation.
I love this method!
I use it all of the time to evaluate my uncertainty analyses. In fact, I include it in every uncertainty budget calculator that I use.
It is really helpful for evaluating uncertainty budgets to find;
• The most significant contributors,
• The least significant contributors,
• Negligible contributors, and
• Errors.
How to Calculate Significance
Calculating the significance of an uncertainty component is not difficult. The process can be completed in only four steps.
To calculate significance, convert your uncertainty components from standard deviations to variances. Next, calculate the sum of squares of all uncertainty components. Then, calculate the ratio of one uncertainty component to the total sum of squares of all the uncertainty components.
Equation
Look at the equation below to calculate significance.
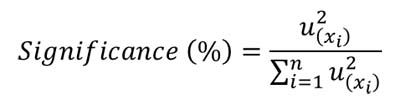
Instructions
To calculate significance, just follow these step-by-step-instructions;
1. Select an uncertainty component,
2. Square the standard uncertainty component to convert it to a variance,
3. Calculate the Sum of Squares for all uncertainty components,
4. Divide the result in Step 2 by the result in Step 3.
Example
To show you how to calculate significance, take a look at the example below.
Imagine that you have 3 uncertainty components;
• CMC Uncertainty,
• UUT Resolution, and
• UUT Repeatability.
The value of each component is provided below as a standard uncertainty;
• CMC Uncertainty: 0.16mV
• UUT Resolution: 0.577mV
• UUT Repeatability: 0.55mV
Now, let’s see how much the UUT Resolution contributed to the total combined uncertainty.
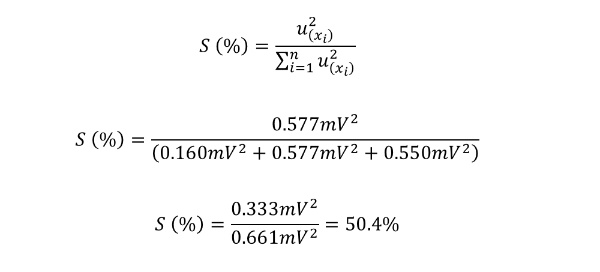
In case you want to work out the equation for yourself, the significance of each uncertainty component is listed below;
• CMC Uncertainty: 3.9%
• UUT Resolution: 50.4%
• UUT Repeatability: 45.7%
How to Calculate Significance in Excel
Calculating significance can be performed using Microsoft Excel. It is a fast and easy way to evaluate your estimates of uncertainty in measurement.
If you use Excel to calculate uncertainty, you can easily add this function to your uncertainty calculator. It will automatically calculate the significance of uncertainty components each time you estimate uncertainty.
In the steps below, you will learn how to add this function to your uncertainty calculator.
1. Square The Standard Uncertainty Component
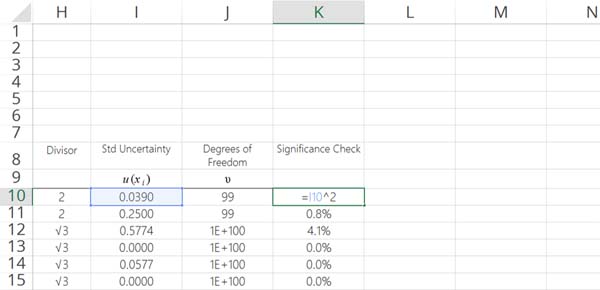
To calculate the significance of an uncertainty component, you must first square the value of the standard uncertainty component. This will convert the standard deviation to variance of the uncertainty component.
2. Calculate The Sum of Squares For All Standard Uncertainty Components
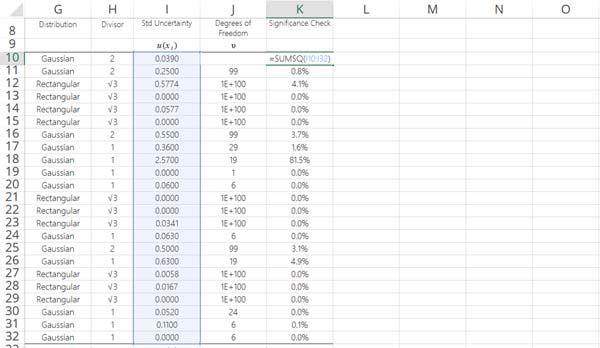
Next, you will calculate the sum of squares for all uncertainty components.
Essentially, you will convert each uncertainty component to a variance and add them all together.
In Microsoft Excel, you will use the sum of squares function, or ‘SUMSQ,’
3. Divide The Result In Step 1 By The Result In Step 2
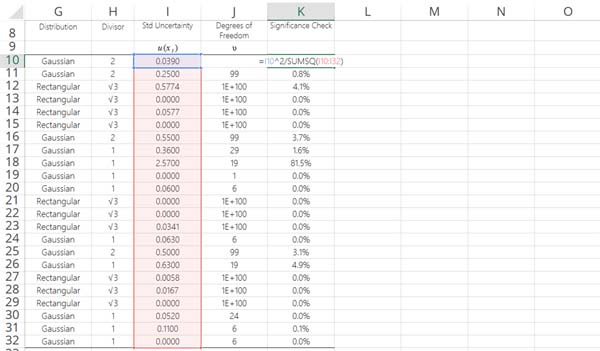
Now, divide the functions given in step 1 by the function in step 2. Your function should look similar to the example below;
=Cell1^2/SUMSQ(Cell2:Cell3)
Where,
Cell1 = standard uncertainty component
Cell2 = First standard uncertainty component
Cell3 = Last standard uncertainty component
How to Validate Your Results
Every time you calculate significance, it is important to double-check your work and validate your results.
Validating your significance calculations is pretty easy. Just add all of your significance calculations together. The result should be 100%.
If your results do not add up to 100%, then you have a problem and must go back to check your equation for errors.
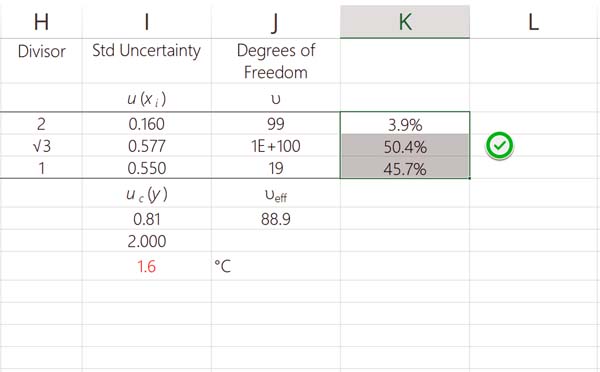
In the example given earlier, significance was calculated for three uncertainty components. Their values were 3.9%, 50.4%, and 45.7%.
When added together, their sum equals 100%.
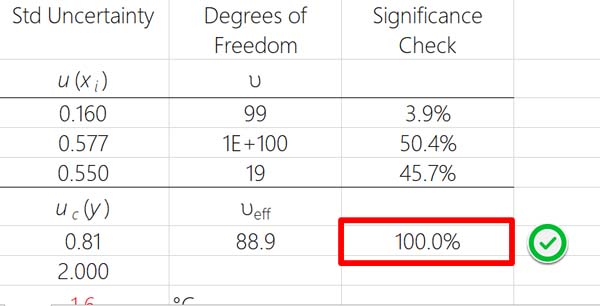
Since the values equal 100%, the calculation is validated to be correct.
How to Add It to Your Uncertainty Budget
Adding significance calculations to your uncertainty budgets can be a very helpful tool for evaluating your uncertainty components.
In fact, I add the function to every one of my uncertainty budgets. It allows me to quickly evaluate my uncertainty calculations.
In this section, I am going to show you how to add this function to your uncertainty calculator; if you use Microsoft Excel. The process is easy. Just follow the steps listed below;
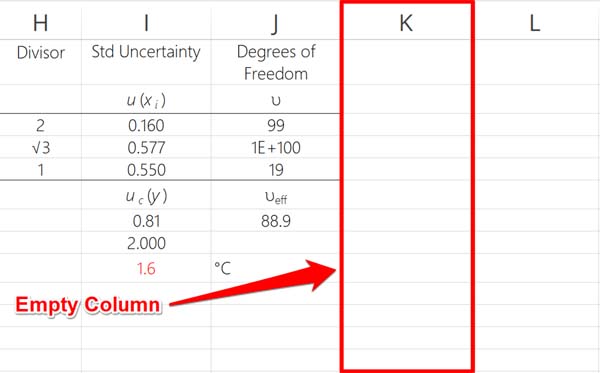
1. Pick An Empty Column Next To Your Uncertainty Budget
Find an empty column next to your uncertainty budget or insert a new column in your uncertainty budget. I prefer to use the last column to the right of the uncertainty calculator.
This column will be used to calculate the significance of your uncertainty components.
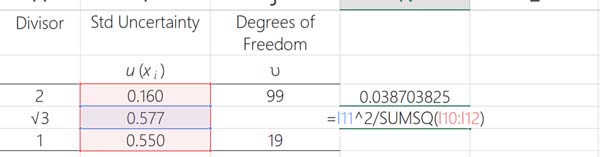
2. Add The Following Excel Function Into a Cell For Each Uncertainty Component
Select the cell that is on the same row as your first uncertainty component and add the Excel function in the image below.

Next, repeat the process and add the function to each row that contains an uncertainty component.
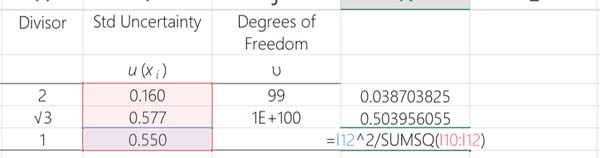
3. Convert The Results To Percentage
Next, you want to convert the values to a percentage. It will help you compare and evaluate results.
Select the cells that contain your significance calculations and click on the percentage button in ‘Home’ tab.
You can also press Ctrl+Shift+% simultaneously to convert the values to percentage.
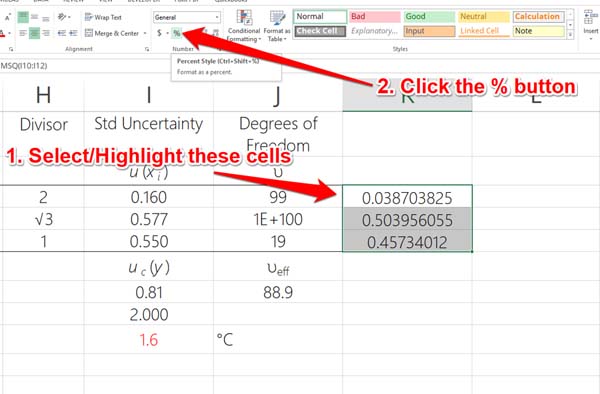
Afterward, your results should look similar to those in the image below.
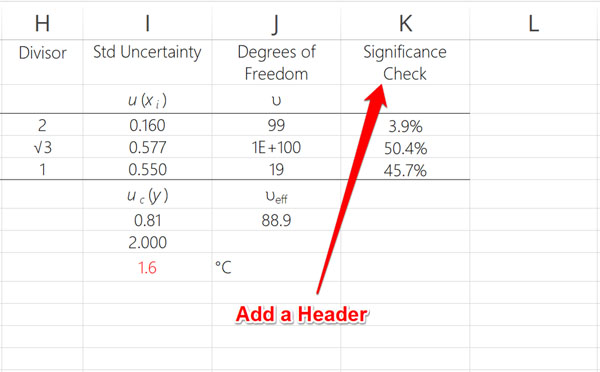
4. Add A Header And Formatting
To help identify your calculations, add a header just above the calculation.
Then, add any necessary formatting to help it blend in with your uncertainty budget or calculator.
5. Calculate The Sum Of The Values
Validating your results is important. All of your significance calculations should add up to 100 percent.
So, add the following Excel function just below your significance calculations.
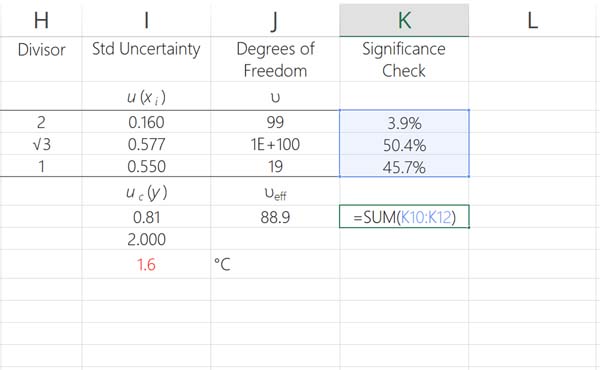
6. Verify The Result Is 100%
Finally, verify the sum of all significance calculation is 100 percent. If it is, you have validated that your calculations are correct.
If the result does not equal 100 percent, you have a mistake. Review each function and fix any errors.
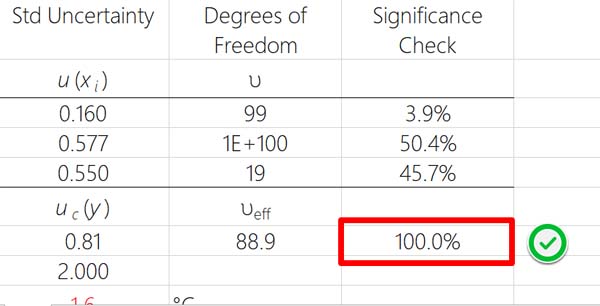
Find Your Most Significant Contributors
The greatest benefit of calculating significance is to determine which uncertainty components contribute the most to your estimated uncertainty.
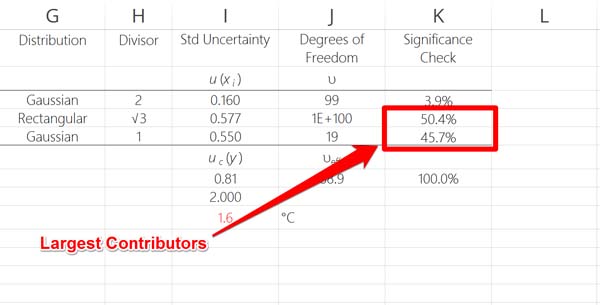
When you identify which components have the largest influence on your measurement uncertainty, you can reduce your uncertainty in measurement by minimizing those components.
Additionally, you can evaluate your largest contributors to verify that you didn’t overstate the uncertainty for a particular component.
Some good questions to ask yourself are;
• Is the value of the uncertainty component correct?
• Is the value of the sensitivity coefficient correct?
• Did I select the right probability distribution and divisor?
• Is the significance calculated correctly?
• Is this typically considered a significant contributor?
Find Your Least Significant Contributors
After you evaluate your largest contributors, you should also review your smallest contributors.
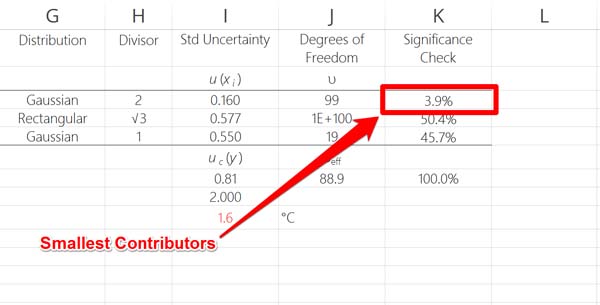
They may not be able to help you reduce your uncertainty in measurement, but you can verify that you did not underestimate uncertainty.
It is quite common for laboratories to underestimate uncertainty. If you have an uncertainty component with little or no significance, you can evaluate it to determine if it is negligible or not.
On the other hand, you can evaluate components considered to be significant contributors to determine whether or not they are in your analysis. If a known significant contributor has a small value for significance, you may want to re-evaluate your estimates to verify that there is not an error.
Some good questions to ask yourself are;
• Is the value of the uncertainty component correct?
• Is the value of the sensitivity coefficient correct?
• Did I select the right probability distribution and divisor?
• Is the significance calculated correctly?
• Is this typically considered a significant contributor?
Common Evaluations of Significant Contributors
After performing thousands of uncertainty analyses, I have noticed some common trends that occur when estimating uncertainty in measurement. By calculating significance, I have been able to identify problems and opportunities for improvement.
Here are some of the most common trends that I have observed.
When laboratories have large or overstated estimates of uncertainty, the most common causes are;
• A Large Reference Standard Uncertainty
• A Large Type A Uncertainty
• A Large Bias
Large Reference Standard Uncertainty
When you discover that the reference standard uncertainty is the largest contributing factor, it is typically caused by sending your equipment to a calibration laboratory that has large CMC uncertainties.
Worse yet, you may find out that the reference standard uncertainty is larger than the accuracy of your equipment.
I see this quite often.
Large Reference Standard Uncertainty can be a sign of;
• Using improper equipment,
• Using improper methods,
• Using unskilled or poorly trained personnel,
• Undesirable environmental conditions, or
• All the above.
To fix this, send your equipment to a calibration laboratory that has a smaller CMC uncertainty. Search your accreditation body’s database to find a laboratory with uncertainties that meet your requirements.
If you are unsure, contact the laboratory and ask questions. Also, you can add statements to your purchase orders to have your equipment calibrated in accordance with uncertainty statements advertised in the laboratory’s scope of accreditation.
Reducing the calibration uncertainty of your equipment can have a significant impact on your estimation of measurement uncertainty.
Large Type A Uncertainty
If you notice that repeatability and(or) reproducibility contribute significantly to your estimated uncertainty, it may be caused by one or more technicians lacking the skill to achieve repeatable measurement results.
To fix this, provide additional training to laboratory personnel to ensure that they are implementing good measurement practices. Train your personnel to perform measurement processes exactly the same way to reduce the amount of variability in their measurement results.
Dedicating 10 to 30 minutes for training can have a big impact on your measurement results.
Additionally, review your measurement methods and(or) procedures for improvement opportunities. One extra step may dramatically improve your measurement results.
Watch your personnel perform a measurement process while following along with the procedure. Look for opportunities to add value and improve the process.
Furthermore, ask your personnel what tips and tricks they use when performing the process and consider adding them to your procedures. If you open a method or procedure and find handwritten notes, it may be a good indicator that you should update your procedures.
By improving operator skills and measurement methods, you can reduce the variability and uncertainty in measurement results.
Large Bias or Systematic Error
If you evaluate your uncertainty budgets and discover that bias is your most significant contributor, you may have a problem.
Take a look at your calibration reports. You may discover that your measurement equipment is within specifications but performing close to its tolerance limits.
When this happens you not only run the risk of having large uncertainty estimates, you can also be at risk for reporting bad results in subsequent tests and(or) calibrations.
If you are not sure what I am referring to, check this article on compliance with specifications.
To fix this, adjust your measurement equipment during calibration to minimize bias.
For in-house calibrations, establish a threshold to perform adjustments. For example, you can establish a threshold to adjust equipment when measurement performance exceed 70% of specifications.
If you send your equipment to another laboratory for calibration, make sure that you request, in writing, that you want your equipment adjusted if it exceeds a defined percentage of the specification.
Talk to the laboratory during to contract review process to see what options they may be able to provide and make sure to that you get your requirements in writing. A good place to have it written is in the laboratory’s quote and in your purchase order.
By reducing bias, you may be able to dramatically reduce you estimations of uncertainty in measurement.
Disclaimer: This only pertains to uncertainty analyses that contain estimates of bias. If you use reference values from your certificates of calibration to compare to subsequent measurement results, you should not need to consider bias in your uncertainty analysis. However, if you assume that a nominal value is true and make no correction for error, then you should include an estimate of bias in your uncertainty budgets.
Conclusion
Finding significant contributors to measurement uncertainty is great way to evaluate your uncertainty budgets.
The best way to find significant contributors to calculate a parameter that I call significance. Calculating significance is fairly easy and can help you quickly evaluate your uncertainty calculations.
If you calculate uncertainty using Microsoft Excel, you can add the function to your uncertainty budgets to automatically calculate significance.
Use the instructions and tips in this guide to calculate significance and find significant contributors. It can help you evaluate your calculations and improve your estimates of measurement uncertainty.
Then, leave a comment and let me know if it helped you evaluate your uncertainty analyses. If not, let me know how you evaluate measurement uncertainty.




4 Comments