
Introduction
Resolution Uncertainty is a factor that contributes to uncertainty in measurement. It’s influence should be considered in every uncertainty budget. However, evaluating resolution uncertainty can vary depending on several factors. So, I have created this guide to help you appropriately identify and evaluate the resolution uncertainty of various measurement equipment.
In this guide, I am going to teach everything that you need to know about resolution uncertainty and more; it is more complex than you ever imagined. To help you quickly find answers to your questions, use the link below to skip ahead.
- What Is Resolution Uncertainty
- Why Is Resolution Uncertainty Important
- Resolution Uncertainty And Uncertainty Analysis
- Resolution Uncertainty Equations
- How To Calculate Resolution Uncertainty By Device Type
- Convert Resolution Uncertainty To Standard Uncertainty
- Overstating And Understating Uncertainty In Measurement
- Examples Of Resolution Uncertainty With Pictures
What is Resolution Uncertainty
Resolution uncertainty is the uncertainty in measurement contributed by resolution of measurement equipment.
Why is Resolution Uncertainty Important
Resolution uncertainty is important because it considers the limitations of measurement equipment. The accuracy, precision, and capability of your measurements are limited by the resolution of the measurement standard and unit under test.
No matter how careful or scientific, you measurement results are limited by the resolution of your measurement standards and the unit under test.
It is important to consider all equipment in the measurement system. The device with the worst resolution will limit your measurement capability.
For example, you can compare the voltage output of a multifunction calibrator (e.g. Fluke 5700A) to a 3.5 digit Multimeter, the resolution of unit under test will have a considerable influence on the measurement result and associated uncertainty.
In another example, you can compare the length of a gage block to a digital calibrator, but the resolution of the digital caliper will affect the measurement result and associated uncertainty; even if you are using a grade 0 gage block.
In both examples, industrial measurement equipment were calibrated using precision equipment and the measurement result and measurement uncertainty were significantly influenced by the poor resolution of the unit under test.
For this reason, resolution uncertainty is considered important, regardless of whether or not it’s influence is significant to the calculated uncertainty in measurement.
Resolution Uncertainty and Uncertainty Analysis
Resolution uncertainty is a factor that should be considered in your uncertainty analysis. However, you have to consider all of the measurement equipment in your measurement system.
Simple Calibrations
For simple measurements or calibrations, you may only have two measurement devices; the measurement standard and the unit under test. In this scenario, you need to consider the resolution of both the measurement standard and the unit under test.
If you performing measurements or calibrations where the type of unit under test is always the same, you should include the resolution of the unit under test in your uncertainty budget to your CMC uncertainty calculations.
On the other hand, if you are performing measurements and calibrations where the unit under test can routinely change, you should omit the UUT resolution from your CMC Uncertainty estimates. Instead, you should include the UUT resolution later when calculating calibration uncertainty in accordance with ILAC P14.
This way you are not overestimating your uncertainty in measurement by considering the resolution of two UUT’s.
Complex Calibrations
When performing complex calibrations, you will likely have several measurement standards involved in your calibration process plus a unit under test. In this scenario, you need to consider the resolution of every measurement standard in your process.
If your measurement standards have different units of measurement, you will need to perform additional work to calculate sensitivity coefficients or fractional uncertainty.
When using sensitivity coefficients or fractional uncertainty, be sure to follow the rules of propagation for uncertainty analysis.
Similar to simple calibrations; if the type of UUT in your calibration process does not change, you should include the UUT resolution in your CMC uncertainty analysis.
If your calibration process can be used to calibrate several different types of UUT’s, then you omit UUT Resolution from your CMC uncertainty analysis and consider it later when calculating calibration uncertainty.
Resolution Uncertainty Equation
When determining resolution uncertainty, there are several equations that can be used to evaluate the resolution of measurement equipment. The biggest challenge for many people is deciding which equation should used.
To select the appropriate equation, it is important to evaluate these factors;
- Type of Device (e.g. digital display, analog scale, or artifact)
- Theory of Operation
- Measurement Resolution
Full Digit/Scale Resolution
The equation below is used when the full resolution of the measurement equipment is considered to contribute to uncertainty in measurement.
In this equation, the resolution of the measurement device is the resolution uncertainty.
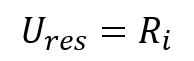
Ures = Resolution Uncertainty
Ri = Resolution of instrument scale
Half Digit/Scale Resolution
The equation below is used when half of the resolution of the measurement equipment is considered to contribute to uncertainty in measurement.
In this equation, the resolution of the measurement device is divided by two to calculate the resolution uncertainty.
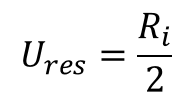
Ures = Resolution Uncertainty
Ri = Resolution of instrument scale
Precision Scale Resolution
The equation below is used when estimating the resolution uncertainty of analog scales and devices.
In this equation, the resolution of the measurement device is divided by the estimated fineness of the analog scale.
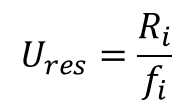
Ures = Resolution Uncertainty
Ri = Resolution of instrument scale
fi = fineness that scale divisions can be sub-divided
This equation is reserved for experienced metrologists and technicians who are capable of properly estimating the fineness of the analog scale.
When working with analog devices, many experts recommend to divide the resolution of the analog scale in half. This may work for many devices, but what if half the distance between scale markers exceeds specifications and tolerances?
In this scenario, the half-digit resolution method fails to adequately estimate resolution uncertainty. Instead, you should consider how finely you can estimate the resolution of the scale between the markers.
How to Determine Fineness
To accomplish this, you need to consider the following factors;
- The scale resolution;
- The width of the scale markers; and
- The width of the dial, pointer, or indicator.
1. Determine the resolution of the analog scale;
2. Evaluate the width of the scale marker and the dial pointer;
3. Determine the fineness: how many times the scale resolution can be sub-divided;
a. determine how many scale markers can fit between the scale markers;
b. determine how many dial pointers can fit between the scale markers;
c. choose the smallest number. This is the value for fineness.
4. Divide the resolution of the analog scale (from step 1) by the fineness of the scale (from step 3c).
Calculate Resolution Uncertainty by Device Type
Resolution uncertainty is affected by the type of measurement equipment being evaluated. Below, you will find step-by-step instructions for determining the resolution uncertainty of various measurement devices.
How to Determine Resolution Uncertainty of Digital Devices
To find the resolution of measurement equipment with a digital display, just
- Find the least significant digit (Hint: it’s the last number on the right-hand side);
- Determine the smallest incremental change (e.g. 1, 2, 5, etc.);
- Determine whether the instrument counts or rounds the last digit;
- Divide the resolution by 1 for counted values or 2 for rounded values.
How to Determine Resolution Uncertainty of Analog Devices
To find the resolution of measurement equipment with an analog scale or display, just
- Find the minimum scale interval (i.e. distance between the scale markers);
- Observe the width of the scale marker and the dial pointer (if equipped);
- Determine how many times the scale can be subdivided (e.g. 1, 2, 5, etc.);
- Divide the resolution of the scale by the value determined in step 3.
How to Determine Resolution Uncertainty of Artifacts
To find the resolution of measurement equipment without a scale or display, just
- Refer to the artifact’s calibration report;
- Find the reported value and uncertainty of the artifact.
- Determine which value has less resolution.
- Select the value with the least resolution.
Convert Resolution to Standard Uncertainty
When converting resolution uncertainty to standard deviation equivalents, there are two equations that are widely accepted for use. The first equation divides the resolution by the square root of 3 and the second equation divides the resolution of the square root of 12.
Determining which that you should use depends on how you decide to evaluate resolution uncertainty. So, I will explain this in more detail below.
The probability distribution associated with the resolution measurement equipment is the Uniform or Rectangular distribution. Therefore, the resolution is divided by the square root of three and has an infinite degrees of freedom.
PRO TIP: To express infinity, I like to use a Googol or a one followed by 100 zeros (i.e. 1.0E+100).
Standard Method to Convert Resolution to Standard Uncertainty
When converting to standard uncertainty, it is common to use the standard method. In this method, you will divide the resolution by the square root of 3.
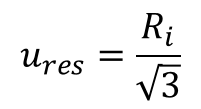
Ures = Resolution Uncertainty
Ri = Resolution uncertainty of measurement equipment
This method is best used when you have already evaluated and sub-divided the resolution of your measurement standards and unit under test. Whenever you are in doubt, use the standard method.
Alternative Method to Convert Resolution to Standard Uncertainty
Sometimes, you may want to evaluate resolution uncertainty as a half digit. Rather than divide the resolution by 2 and then by the square root of 3, you can convert it to a standard deviation equivalent by dividing resolution by the square root of 12.
If you are unfamiliar with this method, give it a try. You will find that the result is the same.
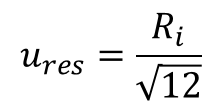
Ures = Resolution Uncertainty
Ri = Resolution of instrument scale
This method is best used when you are evaluating the resolution of your measurement standards and unit under test as a half-digit or half-scale resolution. If resolution is evaluated any other way, use the standard method.
Overstating and Understating Uncertainty in Measurement
It is never wise to overstate or understate estimates of uncertainty in measurement. However, it happens more often than you think; and, mostly by accident. So, it is important to consider how you evaluate resolution uncertainty.
It is very easy to understate uncertainty in measurement if you decide to subdivide the resolution of your measurement standards or unit under test. Additionally, it is just as easy to overstate uncertainty in measurement if you decide to not to subdivide. Therefore, you need to evaluate your estimated uncertainty calculations to verify that you do not overstate or underestimate uncertainty.
To help you out, I will give you two common scenarios below to help you prevent overstating or understating uncertainty.
Understating uncertainty is more common when evaluating lower resolution digital devices. For example, when the uncertainty of your measurement process is much better than the resolution of the unit under test and you decide to evaluate UUT resolution as a half-digit, you are more likely to understate the uncertainty of your measurement results.
Overstating uncertainty is more common when evaluating low resolution analog devices. For example, when the uncertainty of your measurement process is much better than the resolution of the unit under test and you decide to not subdivide the UUT resolution, you are more likely to overstate the uncertainty of your measurement results.
In my opinion, I never subdivide the resolution of digital devices where the uncertainty estimate will be less than the resolution of the UUT. Additionally, I always subdivide analog scales, where practical, to avoid reporting an uncertainty estimate that is larger than the tolerance of the measurement.
So, take these points into consideration and use your best judgment next time you calculate uncertainty in measurement.
Resolution Uncertainty Examples
Evaluating resolution uncertainty is not as easy as most people think it is. There is a lot to take into consideration when evaluating resolution that many take for granted.
To help you better understand how to evaluate resolution uncertainty, I have decided to give you plenty of examples. In this section, you will see me calculate the resolution uncertainty of several different types of devices. Use these examples to help you calculate resolution uncertainty for your measurement results and calibrations.
Now, understand that these results below are subjective; they are my opinion. What one metrologist, scientist, or technician determines as the resolution uncertainty may not agree with another. It is subject to interpretation, capability, and skill. So, be sure to use your best judgment and common sense.
Digital Multimeter Resolution Uncertainty

The digital multimeter in the image above has a resolution of 0.001 VDC. Since the last digit is rounded, it is acceptable to divide the resolution by 2. This makes the resolution uncertainty 0.0005 VDC.
Digital Pressure Gauge Resolution Uncertainty

The digital pressure gauge in the image above has a resolution of 0.1 psig. Since the last digit is rounded, it is acceptable to divide the resolution by 2. This makes the resolution uncertainty 0.05 psig.
Digital Scale / Analytical Balance Resolution Uncertainty

The digital scale or analytical balance in the image above has a resolution of 0.0001 g. Since the last digit is rounded, it is acceptable to divide the resolution by 2. This makes the resolution uncertainty 0.00005 g.
Digital Stopwatch Resolution Uncertainty

The digital stopwatch in the image above has a resolution of 0.01 sec. Since the last digit is counted, it is not acceptable to divide the resolution by 2. Instead, the resolution should be divided by 1 or remain the same as the resolution. This makes the resolution uncertainty 0.01 sec.
Digital Caliper Resolution Uncertainty

The digital caliper in the image above has a resolution of 0.0005 in. Since the last digit is rounded, it is acceptable to divide the resolution by 2. This makes the resolution uncertainty 0.00025 in.
Digital Flowmeter Resolution Uncertainty

The digital flowmeter in the image above has a resolution of 0.01 lpm. Since the last digit is rounded, it is acceptable to divide the resolution by 2. This makes the resolution uncertainty 0.005 lpm.
Analog Pressure Gauge Resolution Uncertainty

The analog pressure gauge in the image above has a resolution of 1 psig. Since the scale markers are very close together, it is acceptable to divide the resolution by 2. This makes the resolution uncertainty 0.5 psig.
Analog Pressure Gauge Resolution Uncertainty

The analog pressure gauge in the image above has a resolution of 2 psig. Since the scale markers are spaced far apart, it is acceptable to divide the resolution by 4. I believe that you can fit 4 markers in between the marker intervals. This makes the resolution uncertainty 0.5 psig.
Analog Magnehelic Resolution Uncertainty

The analog magnehelic gauge in the image above has a resolution of 0.2 inH2O. Since the scale markers are very close together, it is acceptable to divide the resolution by 2. This makes the resolution uncertainty 0.1 inH2O.
Liquid in Glass Thermometer Resolution Uncertainty

The liquid-in-glass thermometer in the image above has a resolution of 1 °C. Since the scale markers are very close together, it is acceptable to divide the resolution by 2. This makes the resolution uncertainty 0.5 °C.
Dial Indicator Resolution Uncertainty

The dial indicator in the image above has a resolution of 0.001 in. Since the scale markers are spaced far apart, it is acceptable to divide the resolution by 5. I believe that you can fit 5 markers in between the marker intervals. This makes the resolution uncertainty 0.0002 in.
Torque Wrench Resolution Uncertainty

The torque wrench in the image above has a resolution of 1 in-lb. Since the torque wrenches minimum setting interval is 1 in-lb, it is acceptable to divide the resolution by 2. This makes the resolution uncertainty 0.5 in-lb.
Torque Screwdriver Resolution Uncertainty

The torque wrench in the image above has a resolution of 5 in-lb. Since the torque wrenches minimum setting interval is 2 in-lb, it is acceptable to divide the resolution by 5. This makes the resolution uncertainty 1 in-lb.
Dry Gas Meter Resolution Uncertainty

The analog dry gas meter in the image above has a resolution of 0.001 CFH. Since the scale markers are spaced far apart, it is acceptable to divide the resolution by 5. I believe that you can fit 5 markers in between the marker intervals. This makes the resolution uncertainty 0.0002 CFH.
Variable Area Flowmeter Resolution Uncertainty

The variable area flowmeter in the image above has a resolution of 0.05 CFM. Since the scale markers are spaced far apart, it is acceptable to divide the resolution by 5. I believe that you can fit 5 markers in between the marker intervals. This makes the resolution uncertainty 0.01 CFM.
Burette Bubble Flowmeter Resolution Uncertainty

The burette bubble flowmeter in the image above has a resolution of 0.2 mL. Since the scale markers are very close together, it is acceptable to divide the resolution by 2. This makes the resolution uncertainty 0.1 mL.
Spring Scale / Force Gauge Resolution Uncertainty

The analog spring scale or force gauge in the image above has a resolution of 1 lbf. Since the scale markers are spaced far apart, it is acceptable to divide the resolution by 3. I believe that you can fit 3 markers in between the marker intervals. This makes the resolution uncertainty 0.33 lbf.
Calibration Mass Resolution Uncertainty

The calibration mass or weight in the image above has a measurement result reported with a resolution of 0.0000001 g. However, the associated measurement uncertainty reported in the calibration certificate has a resolution of 0.000001 g.
Since the reported measurement uncertainty has less resolution, the measurement result should have been rounded to match the resolution of the uncertainty in measurement (in accordance with ILAC P14 policy). Therefore, the appropriate resolution should be 0.000001 g.
Additionally, I do not recommend subdividing the resolution of artifacts, so the resolution uncertainty should match the resolution of the measurement result or 0.000001 g.
Gage Block Resolution Uncertainty

The gage block in the image above has a measurement result reported with a resolution of 0.1 µin. Additionally, the associated measurement uncertainty reported in the calibration certificate has a resolution of 0.1 µin.
Since the reported measurement uncertainty has the same resolution as the measurement result, the resolution uncertainty should be 0.1 µin.
I do not recommend subdividing the resolution of artifacts, so the resolution uncertainty should match the resolution of the measurement result or 0.000001 g.
Conclusion
Resolution uncertainty is an important influence for estimating uncertainty in measurement. With advancements in technology and reduction in tolerances, knowing how to determine and evaluate the resolution of measurement equipment is becoming increasingly more important. In this guide, I have provided you with everything that you need to know to properly evaluate resolution uncertainty.
Now, apply what you have learned from this guide and tell me your biggest frustration with resolution uncertainty.




7 Comments