Moist Air Density: What is it and How to Calculate it

 
 

Introduction

Do you need to calculate moist air density for your measurements or calibrations?

If so, this guide is for you.

From my experience in an accredited calibration lab and as a measurement uncertainty consultant, I used to calculate moist air density all of the time. It is used in many common measurement functions related to:

• Mass,
• Volume,
• Pressure,
• Flow, and
• Sound.

Most of the time, air density calculations are needed for air buoyancy correction of mass or dead weight force. Other times it is used to standardize volumetric flow measurements or correct pressure and sound level measurements.

Knowing how to calculate air density and its associated uncertainty can be vital for some labs. So, I put this guide together to serve as a quick reference to the following information:

 

 
 

What is Moist Air Density

The density of air or atmospheric density, represented by ρ (the rho symbol), is the mass per unit volume of Earth’s atmosphere at a given point and time.

Moist air density, also known as humid air density, takes into account the amount of water content or moisture in the air.

In many cases, measurements are made in humid air (not dry air). Therefore, it is not appropriate to use the density of dry air. Instead, you should use moist air density. Otherwise, your measurement results are prone to error.

 
 

Common Relationships of Air Density

Below are some common relationships between air density and other factors.

• Air density is inversely proportional to changes in Altitude
• Air density is directly proportional to changes in Pressure
• Air density is directly proportional to changes in Volume
• Air density is inversely proportional to changes in Temperature
• Air density is inversely proportional to changes in Humidity

Directly proportional means the two quantities will increase or decrease together at the same rate. For example, if atmospheric pressure increases, then air density will also increase.

Inversely proportional means when one quantity increases or decreases, the other quantity changes in the opposite direction at a rate that maintains a constant product. For example, if air temperature increases, then air density will decrease and vice-versa.

 
 

Air Density at Reference Temperature and Pressures

The table below gives air density at common standard and normal temperature and pressure references. There are plenty more, but these the most common that I have used. Each of these values were calculated using the simplified CIPM formula, so they subject to some uncertainty (I’ll cover on this later).

Standard Temperature and Pressure (101.325 kPa, 0 °C, 0%RH)	1.29269 kg/m3
Normal Temperature and Pressure (at sea level) (101.325 kPa, 15 °C, 0%RH)	1.22539 kg/m3
Normal Temperature and Pressure (101.325 kPa, 0 °C, 0%RH)	1.19929 kg/m3
Normal Temperature and Pressure (14.696 psia, 70 °F, 0%RH)	0.0748863 lb/ft3
Normal Temperature and Pressure (101.325 kPa, 25 °C, 50%RH)	1.17736 kg/m3

 
 

Why is Air Density Important

Air density is important because it is used in many scientific and metrological applications. Whenever accuracy and precision in test or calibration results are critical, an accurate estimate of air density is necessary.

Therefore, you should not use a typical estimate of 1.2 kg/m³. It is not appropriate for laboratory activities where minimal measurement uncertainty is required.

Below, I have created a list of various measurement functions where air density is commonly used to ensure accurate measurement results.

It is used in many scientific applications, including:

• Air Buoyancy Correction
• Torque with lever, dead weight system
• Pressure with dead weight tester
• Force via dead weight
• Mass calibration
• Scale calibration
• Correction Factors
• Pipette calibration, Z correction factor
• Volumetric Capacity Measures
• Volumetric Flow (Liquid and Gas)
• Mass Flow (Liquid and Gas)
• Relative Humidity
• Pressure measured by transducers or manometers
• Speed of Sound
• Sound level measurement
• Length and Flatness calibration using a Laser – Refractive Index of Air
• Flatness calibration using an Autocollimator – Refractive Index of Air

 
 

Important Documents About Air Density

This section includes a list of important documents related to the Air Density formula. There are other documents, but these are the best resources for anyone searching for the density of moist air formula and its associated uncertainty.

 

Proceedings of the 96th Meeting of the CIPM (2007)

This document is the English version of the results from the International Committee for Weights and Measures meeting held November 7th through the 9th of 2007. Section 8.2 includes information about the presentation on the new air density formula.

 

Revised formula for the density of moist air (CIPM 2007) – NIST

This article from Metrologia magazine (Volume 45, 2008, pages 149-155) covers the following information:

• Section 2.1: The CIPM-2007 equation
• Section 2.2: Uncertainty of the CIPM-2007 equation
• Section 3: Comparison with the CIPM-81/91 equation

 

OIML R111-1 – Weights of classes E1, E2, F1, F2, M1, M1–2, M2, M2–3 and M3

Annex E: CIPM formula and an approximation formula
In the OIML R111-1, Annex E, you will find the following information:

• Annex E.1: The CIPM formula for moist air density
• Annex E.3: The approximation formula for air density (simplified CIPM formula)

 

EURAMET CG-18 – Guidelines on the Calibration of Non-Automatic Weighing Instruments

Appendix A – ADVICE FOR ESTIMATION OF AIR DENSITY
In Appendix A of the Euramet CG-18, you will find information for the estimation of air density, including:

• Appendix A1.1: Simplified version of the CIPM formula,
• Appendix A2: Uncertainties related to Pressure, Temperature, and Humidity,
• Appendix A3: Uncertainty of Air Density

 
 

How to Calculate Moist Air Density

To calculate moist air density, you have two options; use the:

1. CIPM 2007 formula, or
2. Simplified CIPM 2007 formula.

Many standards and guides recommend using simplified CIPM formula; and, I agree. It is the best option for most laboratories and their activities.

So, I will focus this guide on showing you how to calculate moist air density using the simplified CIPM formula. In this section, you will learn the following information:

1. Moist Air Density formula (Simplified CIPM formula),
2. Step-by-step instructions to calculate air density,
3. Evaluation of uncertainty for moist air density, and
4. Example calculations.

 
 

Moist Air Density Formula

Below, you will see the simplified CIPM formula for calculating moist air density. This formula is most commonly found in the OIML R111 and EURAMET CG-18 guides.

 
 

Simplified version of CIPM-formula, exponential version

From OIML R111 [4], section E3

 
 

 
 

Instructions for Calculating Moist Air Density

Follow the instructions below to calculate the moist air density for your location and environmental conditions. I have broken down the steps based on order of operations to ensure your calculations are accurate.

1. Find the barometric pressure, air temperature, and relative humidity.
2. Multiply the barometric pressure by 0.34848.
3. Multiply the relative humidity by 0.009.
4. Multiply the air temperature by 0.061.
5. Calculate the exponential (exp function) of the result from Step 4.
6. Multiply the results of Step 3 and Step 5.
7. Subtract the result of Step 2 by Step 6.
8. Add 273.15 to the air temperature.
9. Divide the result of Step 7 by Step 8.

 
 

Example of Calculating Moist Air Density

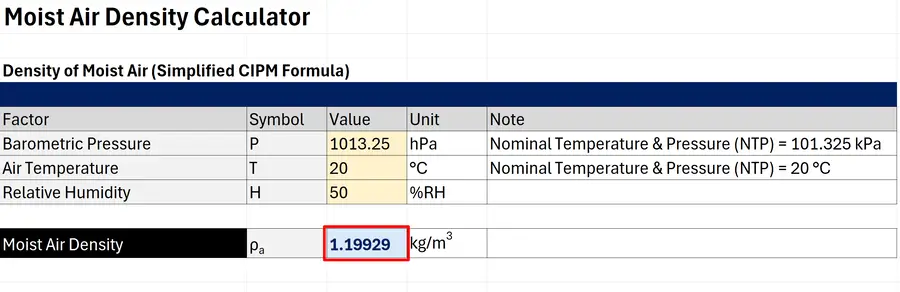
In the image below, I calculated the density of moist air using the simplified CIPM formula.

For this example, the following environmental conditions used:

• Barometric Pressure: 1013.25 hPa
• Air Temperature: 20 °C
• Relative Humidity: 50 %RH

The calculator gave a result of 1.19929 kg/m³.

Look at the red rectangle in the image below to see the result.

 
Click here to download the
Air Density Calculator for free!

 
 

Uncertainty of Moist Air Density

When you need to calculate moist air density, you usually need to evaluate the uncertainty associated with it. Typically, this to support another uncertainty analysis.

To estimate the uncertainty of air density, you need to consider four factors. These are:

1. Barometric Pressure Uncertainty,
2. Air Temperature Uncertainty,
3. Relative Humidity Uncertainty, and
4. Formula Uncertainty

The best guide to estimate uncertainty for air density is the EURAMET CG-18. It covers everything you need to know, plus it includes a quick reference table that you can quickly find the uncertainty.

 
 

Air Density Uncertainty Formula

Below, you will find the section EURAMET CG-18 that gives the formula for calculating the uncertainty of air density.

If formula A3-1 looks intimidating, then you may want to use the simplified formula given in A3-2 at the bottom of the image.

 
 

Method #1: Easy Way to Calculate Air Density Uncertainty

If you are not interested in evaluating your own air density uncertainty, then you can use the table below. It is the table from EURAMET CG-18, Appendix A.

 
 

Instructions

Using the above table, follow the instructions below:

1. Calculate your air density,
2. Find the temperature and humidity variations similar to your environment,
3. On the same row, find the air density uncertainty sensitivity coefficient (last column),
4. Multiply your air density by the uncertainty sensitivity coefficient.

The result is your air density uncertainty.

 
 

Method #2: More Accurate Way to Calculate Air Density Uncertainty

If you need an accurate estimate of air density uncertainty, then you will need to evaluate it yourself. To do this, you will need to propagate the following the uncertainties through the air density formula:

1. Barometric Pressure Uncertainty,
2. Air Temperature Uncertainty,
3. Relative Humidity Uncertainty, and
4. CIPM Simplified Formula Uncertainty

 
 

Instructions

Using the above table, follow the instructions below:

1. Calculate your air density,
2. Determine the uncertainty associated with the following contributors:
1. Barometric Pressure,
2. Air Temperature,
3. Relative Humidity, and
4. Formula
3. Propagate the uncertainties through the air density formula,
4. Determine the magnitude of each uncertainty in the:
1. same unit of measurement as the air density, or
2. a term relative to the calculated air density (e.g. percent).
5. Convert each uncertainty to a standard uncertainty,
6. Calculate the combined standard uncertainty using the RSS method.

The result is your air density uncertainty at a 68 % confidence interval where k=1.

 
 

Sources of Uncertainty for Moist Air Density

If you plan to calculate the uncertainty of moist air density using method #2 (in the previous section), you need to know the sources of uncertainty and how to evaluate them.

The information in this section is based on EURAMET CG-18, Appendix A and should help you determine the uncertainty associated with the following sources of uncertainty:

1. Barometric Pressure Uncertainty,
2. Air Temperature Uncertainty,
3. Relative Humidity Uncertainty, and
4. CIPM Simplified Formula Uncertainty

 
 

Barometric Pressure Uncertainty

To estimate uncertainty for Barometric Pressure, you have two options. These include:

1. The uncertainty of the barometer used to monitor the environment, or
2. The barometric pressure uncertainty from the CIPM 2007.

 
 

Barometer Uncertainty

If you use a barometer to monitor barometric pressure and calculate moist air density, then use the uncertainty of the barometer’s measurement capabilities.

 
 

Weather Station Barometer Uncertainty

If you do not have a barometer, you can use barometric pressure readings from the local weather station or airport. In this scenario, you do not know the measurement uncertainty associated with the barometric pressure reading.

So, the EURAMET CG-18 claims the standard uncertainty is 10 hPa (at 68% confidence, where k=1).

In the image below, you will see an excerpt about barometric pressure uncertainty from the EURAMET CG-18.

 
Alternatively, the NISTIR 6969, SOP 2 claims the standard uncertainty of atmospheric pressure is 6.65 hPa (at 68% confidence, where k=1). See table 3 in the image below.

 
Either one of these uncertainties may be used in your evaluation. However, I typically use 10 hPa.

 
 

Temperature Uncertainty

To estimate uncertainty for air temperature, you have two options. These include:

1. The uncertainty of the thermometer used to monitor the environment, or
2. The half-interval of the environmental control limits.

 
 

Thermometer Uncertainty

If you monitor the environment with a thermometer and correct your results based on the actual air temperature, then consider using the uncertainty of your thermometer for the temperature uncertainty.

You should be able to find the uncertainty of the thermometer from your uncertainty budgets or scope of accreditation CMC uncertainties.

If none of these are available, then you can use the accuracy of your thermometer as a worst case substitute. However, if temperature is a significant contributor to uncertainty, then you should perform a full uncertainty analysis for measuring temperature with your thermometer to ensure you do not underestimate uncertainty.

 
 

Environmental Control Limits

To estimate uncertainty based on environmental control limits, find the temperature control limits for your laboratory or the activity you are performing.

For example, if the laboratory’s environmental control limits are (18 to 28) °C, then the temperature uncertainty would be ±5 °C.

To calculate this value, simply subtract the upper temperature limit by the lower temperature limit and divide the result by 2. The final result will be the temperature uncertainty based on the half-interval of the environmental control limits.

Characterize the uncertainty as a Type B uncertainty with a rectangular distribution and a divisor equal to the square root of 3 in accordance with the JCGM 100:2008, section 4.3.7.

A simplified formula to determine the standard uncertainty of temperature is shown below.

 
In the image below, you will see an excerpt from the EURAMET CG-18 that supports this evaluation technique. You will notice they simply the divisor (in the formula) using the square-root of 12 which is mathematically the same as two multiplied by the square-root of three.

 
 

Humidity Uncertainty

To estimate uncertainty for humidity, you have two options. These include:

1. The uncertainty of the hygrometer used to monitor the environment, or
2. The half-interval of the environmental control limits.

 
 

Hygrometer Uncertainty

If you monitor the environment with a hygrometer, then consider using the uncertainty of your hygrometer for the humidity uncertainty.

You should be able to find the uncertainty of the hygrometer from your uncertainty budgets or scope of accreditation CMC uncertainties.

If none of these are available, then you can use the accuracy of your hygrometer as a worst case substitute. However, if humidity is a significant contributor to uncertainty (not common), then you should perform an full uncertainty analysis for measuring relative humidity with your hygrometer to ensure you do not underestimate uncertainty.

 
 

Environmental Control Limits

To estimate uncertainty based on environmental control limits, find the humidity control limits for your laboratory or the activity you are performing.

For example, if the laboratory’s environmental control limits for humidity are (20 to 80) %RH, then the humidity uncertainty would be ±30 %RH.

To calculate this value, simply subtract the upper humidity limit by the lower humidity limit and divide the result by 2. The final result is the humidity uncertainty based on the half-interval of the environmental control limits.

Characterize the uncertainty as a Type B uncertainty with a rectangular distribution and a divisor equal to the square root of 3 in accordance with the JCGM 100:2008, section 4.3.7.

A simplified formula to determine the standard uncertainty of humidity is shown below.

 
In the image below, you will see an excerpt from the EURAMET CG-18 that supports this evaluation technique. You will notice they simply the divisor (in the formula) using the square-root of 12 which is mathematically the same as two multiplied by the square-root of three.

 
 

Formula Uncertainty

According to EURAMET CG-18, the uncertainty associated with simplified CIPM formula is the equal to the product of multiplying the air density value by the sensitivity coefficient 0.00024.

For example, multiplying 0.00024 and an air density equal to 1.2 kg/m3 would give you a formula uncertainty of 0.000288 kg/m³.

To simply this, convert the sensitivity coefficient to a percentage or 0.024 % of value.

Also, make sure to realize the uncertainty is a standard uncertainty with a 68 % confidence interval where k = 1.

An excerpt from the EURAMET CG-18 about the formula uncertainty is provided in the image below.

 
 

Summary

Based on the information in this section, I have compiled a list of the sources of uncertainty and their magnitude for common environmental conditions.

In the table below, you will find recommended uncertainties for following types of environments:

• Highly Controlled Lab Environment,
• Typical Controlled Lab Environment,
• Typical Uncontrolled Field Environment, and
• Extreme Uncontrolled Field Environment.

Disclaimer: These are recommended uncertainties for commonly encountered environmental conditions. Your actual uncertainties may be different.

 

Uncertainties for Common Environmental Conditions

Source of Uncertainty	Highly Controlled	Controlled (Typical)	Uncontrolled (Typical Field)	Extreme
Barometric Pressure	± 10 hPa	± 10 hPa	± 10 hPa	± 10 hPa
Temperature	± 2 °C	± 5 °C	± 10 °C	± 20 °C
Humidity	± 10 %RH	± 20 %RH	± 100 %RH	± 100 %RH
Formula	ρa 2×10-4	ρa 2×10-4	ρa 2×10-4	ρa 2×10-4

 
 

Comparison of Methods for Evaluating the Uncertainty of Air Density

Typically, I estimate the uncertainty of air density using a one-factor at a time analysis (OFAT). However, it is much simpler to use the table from the EURAMET CG-18.

The reason I evaluate it myself is because many of my customers have a variety of environmental control limits that do not match CG-18 table.

 
 

One-Factor at a Time Analysis

When I estimate uncertainty, I typically use a one-factor at a time analysis. It is a technique that uses replicate experiments to evaluate the uncertainty of each contributor (one at a time). Some people refer to this as the Kragten method.

So, I evaluated the uncertainty of each variable (input quantity) one at a time to determine the effect on the calculated moist air density. Then, the uncertainties are combined using the RSS method to determine the combined, standard uncertainty (68 % C.I., k=1)

 
 

Full Factorial Experiment

Another technique that I like to use is the Full Factorial experiment design. This method evaluates a combination of replicate experiments at the extremes of each variable (input quantity) to determine the sensitivity coefficients of each variable and a prediction equation for the process.

It is great for optimizing a process and commonly used in robust testing and robust engineering.

So, I designed and implemented a full factorial experiment to determine the sensitivity coefficients of each variable (i.e. Pressure, Temperature, and Humidity). Next, I multiplied the sensitivity coefficients by their associated uncertainty. Then, I combined the uncertainties using the RSS method to determine the combined, standard uncertainty (68 % C.I., k=1).

 
 

Euramet CG-18 Table

Finally, I used the table in Appendix A of the Euramet CG-18 to determine the uncertainty of the calculated moist air density.

 
 

How to use the Table

The table is easy to use. All you need to do is determine your temperature and humidity variations and find them in the table.

For this example, I evaluated a temperature variation of 10 °C and a humidity variation of 100 %RH.

If you look at the second and third column of the table, find the temperature and humidity variations that match your specifications. Then, find the air density uncertainty sensitivity coefficient in the last column on the same row. Finally, multiply the sensitivity coefficient by your air density.

 

 
 

The Results

After evaluating the uncertainty of air density with each method, I decided to compare the results. Surprisingly, the difference between the results was less than 5% (i.e. Typical criteria for a significant contributor to uncertainty).

Therefore, any of the methods used to evaluate uncertainty could be used. Personally, I would recommend using the Table in Appendix A of the Euramet CG-18. It is an easy and fast way to get the uncertainty of air density.

Look at the image below to see standard uncertainty associated with each method. Also, I included the sensitivity coefficients associated with pressure, temperature, humidity, and the formula.

 
When looking at the results, it is important to know the following:

• absolute air density uncertainty is the air density uncertainty given in the same units of measurement as the calculated moist air density;
• relative air density uncertainty is the air density uncertainty given in units relative (i.e. percentage) to the calculated moist air density units of measurement.

 
 

Frequently Asked Questions

Here are answers to common questions people ask about moist air density.

 
 

What is the difference between dry air density and moist air density?

Answer: The difference between air density and most air density is moist air density includes the effects of relative humidity (water content) on air density. Air density commonly refers to dry air density and does not account for water content in the ambient air.

 
 

What is the formula for calculating moist air density?

Answer: The formula for moist air density can be found in the OIML R111 [4], section E3 and Euramet CG-18, Appendix A1.1. The formula is given below:

 

 
 

What is the uncertainty of air density?

Answer: The uncertainty of moist air density is typically between 1 % and 1.5 % of the calculated air density. This is accurate for most well controlled environments. Uncontrolled environmental conditions can have larger uncertainties such as 2.5 % to 3.4 % of the calculated air density.

 
 

What is the uncertainty of atmospheric pressure?

Answer: The standard uncertainty of atmospheric pressure obtained from local weather stations and airports is estimated to equal 10 hPa (68 % C.I., k=1). Evidence of this can be found in the Euramet CG-18, Appendix A2.1. The uncertainty was derived from 20 years of data collected by DWD, the German Meteorological Service.

 
 

Is there a moist air density calculator?

Answer: Yes. We have an Excel moist air density calculator. Also, Omni Calculator has an online moist air density calculator. Use the links below to access them.

• ISOBudgets – Moist Air Density Calculator (Microsoft Excel)
• Omni Calculator – Moist Air Density Calculator (Online)

 
 

What is the moist air density at 20 °C and 101.325 kPa (NTP)?

Answer: The density of humid air at normal temperature and pressure (20 °C, 101.326 kPa, and 50 %RH) is approximately 1.19929 kg/m³.

 
 

What is the moist air density at 0 °C and 101.325 kPa (STP)?

Answer: The density of air at standard temperature and pressure (0 °C, 101.326 kPa, and 0 %RH) is approximately 1.29269 kg/m³.

 
 

Conclusion

Moist air density is an important component that affects many metrologically traceable measurements. When minimal measurement uncertainty is required, using an air density of 1.2 kg/m³ is not appropriate. Therefore, you must calculate the density of air for your environmental conditions.

In this guide, I have covered everything that you need to know, including:

• What is Moist Air Density
• Why is Moist Air Density Important
• Important Documents About Air Density
• How to Calculate Moist Air Density
• Uncertainty of Moist Air Density
• Answers to Frequently Asked Questions

I hope this guide serves as a helpful resource for ISO/IEC 17025 accredited laboratories.

Additionally, make sure to download the:

• Documents referenced in this guide (for your records)
• Excel calculator for moist air density

If I have left anything out of this guide, let me know and I will get it added.