
Have you ever looked at your scope of accreditation and wondered, “How do I calculate uncertainty with this equation?” If so, you are in luck! I am going to show you step by step, how to calculate CMC uncertainty using the equations in your scope.
Over the last two months, I have received a ton of emails and phone calls asking how to calculate uncertainty using the equations published in the laboratories scope of accreditation. Well, I’m about to answer your prayers. Let’s get started.
Scope of Accreditation
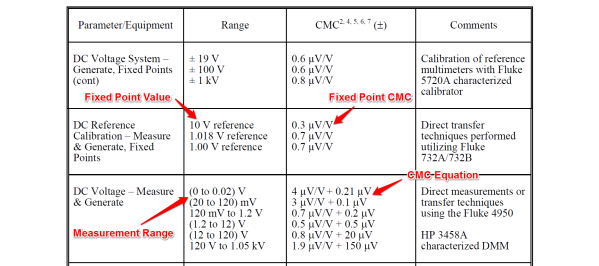
Just to clarify which equations I am writing about, let’s look at several sample scopes of accreditation to see a few examples. Here is an example from Fluke’s Everett Service Center scope of accreditation. If you look below, you will notice both a fixed point CMC uncertainty statement and an equation for the calculation of CMC uncertainty.
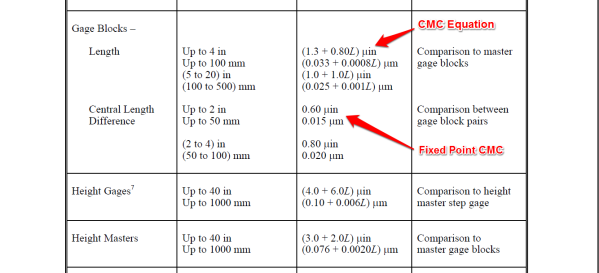
If you perform dimensional metrology, here is an excerpt from Mitutoyo’s scope of accreditation. Notice the difference between a fixed point CMC uncertainty statement and the CMC uncertainty equation.
Uncertainty Equations
Uncertainty equations are just linear equations that characterize the uncertainty of measurement as a function of a range of measurement values. They are typically derived from the use of regression techniques to identify an equation that fits a set of data to a mathematical model. These are commonly referred to as a ‘line of best fit’ because the equation fits a set of data with minimal standard error. However, this is not always the case and we may need to expand our equation a second order for curvature or a third or more orders to account for inflections; but, that is a topic for another post. Here, we will describe only linear or first-order equations.
There are several formulas used to describe linear equations. Some of you may be familiar with the line equation. It converts an input, x, to an output, y, using the coefficient m for slope and the coefficient b for y-intercept.
![]()
If you are familiar with regression analysis and statistics, you may be more familiar with the linear equation that uses the greek letter beta to define the sensitivity or gain coefficient β1 and the offset coefficient β0. This is my equation of choice and I will be using it throughout this article. It is similar to the previous equation. The only difference is letters used to represent the coefficients.
![]()
Calculating CMC Uncertainty
To calculate CMC uncertainty, we need to first identify the appropriate measurement function and range associated with our measurement process. Next, you will want to find the coefficients for sensitivity and offset. Use the image below as a guide.
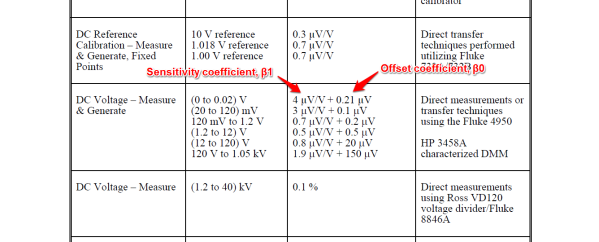
For this example, I have selected to calculate the CMC uncertainty for 10mV. Therefore, we will use the sensitivity coefficients for ‘DC Voltage – Measure & Generate,’ and the range ‘(0 to 0.02) V.’ Now, you are going to plug these coefficients into the linear equation formula that I showed you earlier. It should look like this:
![]()
Since we are estimating the uncertainty for 10mV, it will be our input variable. Replace x with 10mV, but convert it to volts to coordinate with our sensitivity coefficient which is micro-volts per volt. Finally, solve the equation.
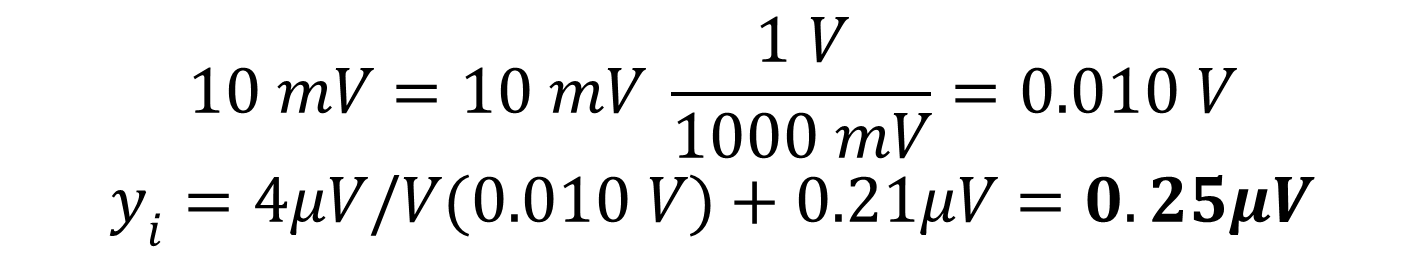
Still confused? Let’s break it down step by step.
1. Identify the measurement process (i.e. Parameter/Function).
‘DC Voltage – Measure & Generate’
2. Select the method or measurement system (i.e. Comments).
‘Direct measurements or transfer techniques using the Fluke 4950’
3. Select the measurement Range (i.e. Range).
‘(0 to 0.02) V’
4. Identify the CMC sensitivity coefficients (i.e. CMC)
Gain coefficient, β1 = 4 μV/V
Offset coefficient, β0 = 0.21 μV
5. Plug the coefficients into the linear equation.
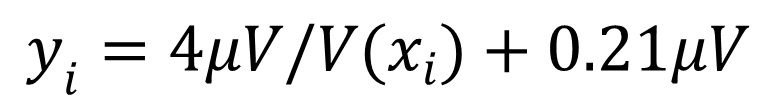
6. Convert the input variable to compatible units of measure.
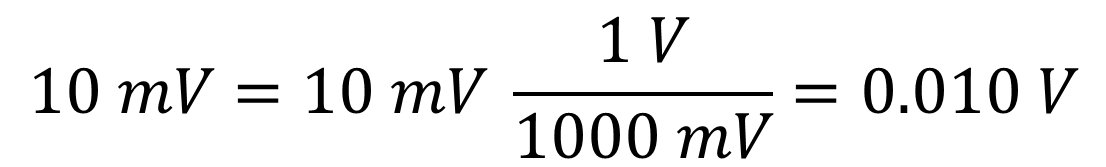
7. Replace xi with the input variable (e.g. 0.01 V).
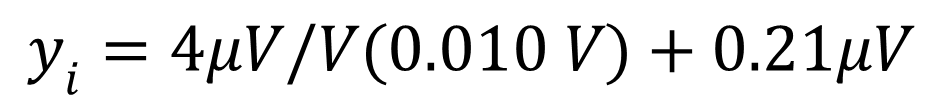
8. Solve for yI.
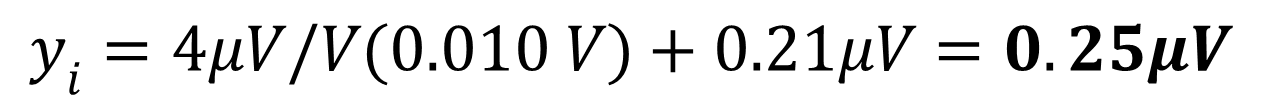
All done! Your CMC uncertainty for our example is 0.25 micro-volts. See, that wasn’t so bad. Let’s try one more using a CMC equation from our dimensional scope shown earlier. So you don’t have to scroll back up, here is the image again.

In this example, let’s estimate the CMC Uncertainty for the length of a 1-inch Gage Block compared to a master gage block.
1. Identify the measurement process (i.e. Parameter/Function).
‘Gage Block – Length’
2. Select the method or measurement system (i.e. Comments).
‘Comparison to master gage blocks’
3. Select the measurement Range (i.e. Range).
‘Up to 4 in’
4. Identify the CMC sensitivity coefficients (i.e. CMC)
Gain coefficient, β1 = 0.80L μin or 0.80 μin/in
Offset coefficient, β0 = 1.3 μin
5. Plug the coefficients into the linear equation.
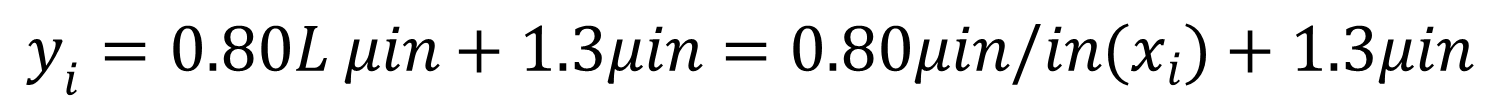
6. Convert the input variable to compatible units of measure.
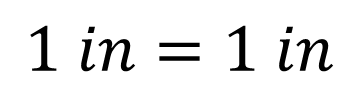
7. Replace L or xi with the input variable (e.g. 1 in).
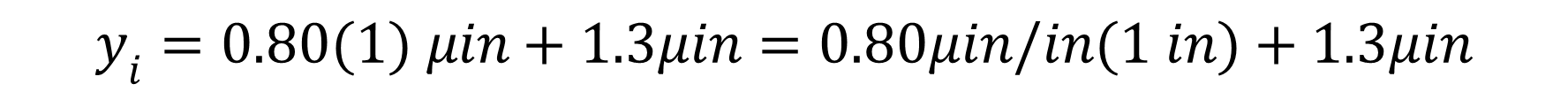
8. Solve for yI.
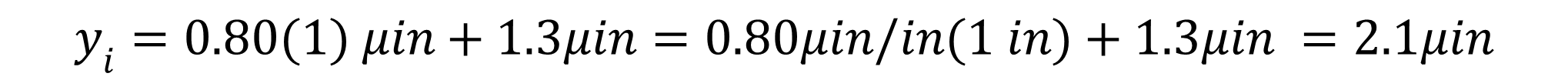
CMC Uncertainty in Excel
Still want more? I don’t blame you. Who wants to calculate CMC uncertainty long-hand; it takes forever. What if I gave you the formulas for performing these calculations in Excel? Then, you could calculate uncertainty faster and easily repeat the process anytime you need.
To begin, select cells for the following parameters and title them. Enter the desired values in the appropriate cells, and input the equation below in the Ucmc cell. You have just created an excel calculator for CMC uncertainty.
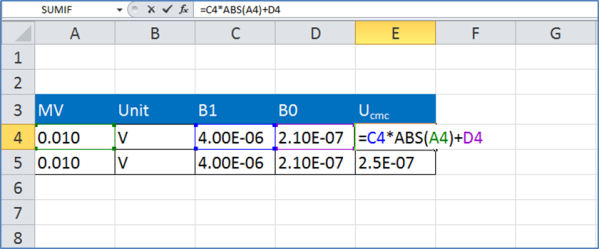
If you plan to calculate uncertainty for a large set of parameters, it is best populate the cells in rows. It is easy to copy and paste rows, and it makes it easier to call values from cells, similar to database fields for use in other spreadsheets.
Conclusion
Calculating CMC Uncertainty is not difficult, but it helps to follow a procedure. I hope this article is helpful to those with inquires and to others who stumble upon this post needing answers. If you need me to elaborate this process further, feel free to contact me at [email protected].
Keep the questions coming; it fuels my editorial calendar for future articles. If you not a subscriber, join now and get new articles sent to your inbox. I do not spam and it’s FREE. What do you have to lose?




5 Comments