Whenever a measurement is performed, the result is never exact. No matter how careful or scientific, every measurement is susceptible to error and uncertainty. A measurement is the best quantitative estimate of an observation constrained by one or more limiting factors. These constraints establish doubt in the observed result and introduce the concept of uncertainty.
Laboratories and manufacturers worldwide perform measurements every day. The results of measurements and the conclusions derived from them impact the quality and safety of products and services used by consumers. Therefore, education and awareness of uncertainty in measurement is more important than ever.
Quantitative measurement data is commonly used to influence and make decisions. With each decision comes an acknowledgement and acceptance of risk. Uncertainty is a parameter that exhibits the quality of measurement data. Understanding the meaning and application of uncertainty will help infuse confidence in decision making.
This following information aims to introduce readers to the concept of uncertainty in measurement results. More information with regard to measurement uncertainty and uncertainty analysis may be found in our technical library.
What is Measurement Uncertainty?
According to the 2012 edition of BIPM’s Vocabulary in Metrology (VIM), the term uncertainty is defined as a non-negative parameter characterizing the dispersion of the quantity values being attributed to a measurand, based on the information used.
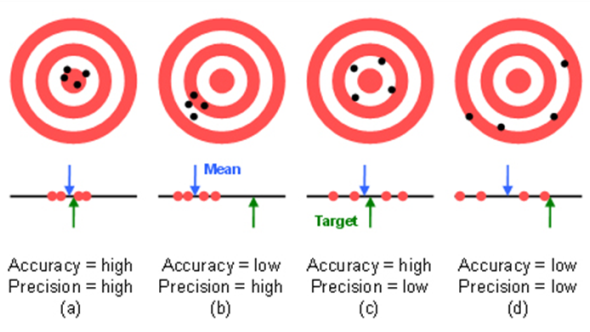
Essentially, the uncertainty of a measurement result is the doubt associated with the measurement result. Regardless of how careful or scientific, all measurements are subject to error and uncertainty. We can never be absolutely certain that a measurement result is true or finite. Therefore, we must establish a boundary for which we are confident that the measurement result will lie between.
Error vs Uncertainty
Error and uncertainty are two terms that have been used interchangeably in the past. However, the meaning of each term is distinctly different.
• Uncertainty is a quantification of the doubt associated with a measurement result. Essentially, it expresses something about its quality.
• Error is the difference between the measured value and the true value of what is being measured.
The Darkness Principle states that everything about a system can not be known. Where we are able to quantify error through empirical experimentation, we can apply a correction. Since we are unable to know the true value, we will never know the error. Any error whose value is not known is a source of uncertainty. Therefore, we must account for what we do not know and what we can not quantify.
Types of Errors
Errors can be classified into two distinct types: random and systematic. The classifications are determined by how the error impacts the measurement result.
• Random error is an error that is random and uncorrelated, which affects the results of repeated measurements. Sources of random error add a component to the measurement result that is unknown.
• Systematic error is an error that affects all measurements in the same way. When random errors are small, it is possible to identify systematic errors.
Types of Uncertainty
Uncertainties can be classified into two distinct types: Type A and Type B. The classifications are determined by how the uncertainty is estimated.
• Type A uncertainties are those evaluated using statistical methods as a result of empirical experimentation.
• Type B uncertainties are those evaluated by means other than statistical methods; past experiments, calibration data, manufacturer’s specifications, etc.
Sources of Error and Uncertainty
A measurement result is never perfect. Internal and external factors impact the ability to achieve the ideal measurement results. These factors are identified as sources of uncertainty.
Some common sources of uncertainty are:
•random errors: repeatability, reproducibility, and stability
•systematic errors: accuracy, bias, drift, etc.
•the measurement system
•the unit under test
•equipment resolution
•traceability: calibration uncertainty
•the measurement process
•operator skill
•environmental conditions: temperature, humidity, pressure, etc.
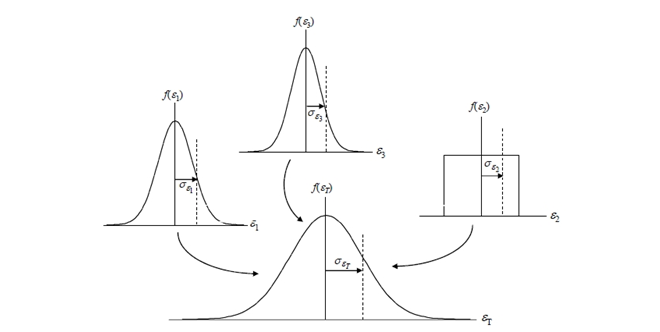
Propagation of Uncertainty
Some physical measurements cannot be accomplished with a single direct measurement. Therefore, the measurement is calculated by the direct measurement of two or more independent variables. When a measurement result requires two or more steps, the estimation of uncertainty requires two or more steps. The following methods should be used to determine how the uncertainties of indirect measurements propagate through the calculations to produce an uncertainty in the final result.
Estimating Uncertainty
Estimating uncertainty is accomplished through the combination and expansion of multiple contributing factors that introduce uncertainty in the measurement result. The Metrology industry typically regards the methods described in the “ISO Guide to the Expression of Uncertainty in Measurement” as the standard which all ISO 17025 accredited laboratories shall adhere.
Uncertainty contributors are combined using the root sum of squares method. Under the Central Limit Theorem, the probability distribution of the combined uncertainty takes the form of a Gaussian or normal distribution. Afterward, the combined uncertainty is expanded to a desired confidence level. In the Metrology Industry, it is common to expand uncertainty to a 95.45% confidence interval, where k = 2.00.
Expressing Uncertainty
According to NIST, a measurement result is only complete when reported with an associated estimate of measurement uncertainty. Therefore, all quantitative measurement results should be expressed with an estimated value of uncertainty. The International Laboratory Accreditation Cooperation (ILAC) has developed and instituted a policy for ISO 17025 accredited laboratories to abide by when expressing measurement uncertainty. The document is the ILAC P-14:12/2010, the “Policy for Uncertainty in Calibration.”
References
1. Taylor, B. N. and Kuyatt, C. E. Nist Technical Note 1297, “Guidelines for Evaluating and Expressing the Uncertainty Measurement Results. Gaithersburg : NIST, 1994.
2. Taylor, John R. An Intoduction to Error Analysis. Sausalito : University Science Books, 1997.
3. Kirkup, Les and Frenkel, Bob. An Introduction to Uncertainty in Measurement. Cambridge : Cambridge University Press, 2006.
4. Dieck, Robert H. Measurement Uncertainty. Research Triangle Park : ISA, 2006.
5. Joint Committee for Guides in Metrology. International Vocabuary in Metrology – Basic and General Concepts and Associated Terms. Sevres Cedex : Bureau International des Poids et Mesures, 2012.
6. United Kingdom Accreditation Service. M3003: The Expression of Uncertainty and Confidence in Measurement. Feltham : United Kingdom Accreditation Service, 2007.




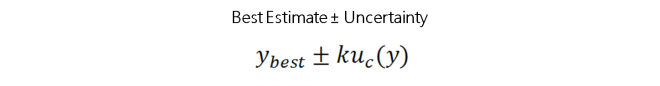




2 Comments