How to Calculate Emissivity Uncertainty

 
 

Introduction

Emissivity is a source of uncertainty that affects IR temperature (i.e. radiation thermometry). It should be included in uncertainty budgets for blackbody calibrators and IR Thermometers. However, many ISO/IEC 17025 accredited laboratories have not included emissivity uncertainty in their budgets because their lab personnel did not know how to evaluate it. Furthermore, many experts, assessors, and accreditation bodies do a poor job of informing laboratories that:

1. It is a significant contributor that should be included in uncertainty budgets, and
2. What resources are available that laboratories should use to evaluate it.

This has led to a recent increasing trend in audit deficiencies related to not including emissivity uncertainty in the uncertainty analysis for IR temperature. So much so, that it made my list of top deficiencies (related to measurement uncertainty) cited last year.

In this guide, you will learn how to calculate emissivity uncertainty related to your infrared temperature measurements. With this information, you should be able to calculate the uncertainty caused by emissivity so you can:

1. Include it in your uncertainty budgets, and/or
2. Correct your temperature measurements.

In either case, this is great information to know. Plus, this will work for both blackbody calibrators and infrared thermometers.

If you need to include this in your uncertainty budgets, keep reading. I am going to break down the process step by step and point you to professional resources that will back up the evaluation.

Plus, I have created an emissivity uncertainty calculator based on this method so you can estimate uncertainty faster.

 
 

What is Emissivity

According to the National Physical Laboratory (NPL) in the UK, emissivity is defined as the ratio of the energy radiated from a material’s surface to that radiated from a perfect emitter, known as a blackbody, at the same temperature and wavelength and under the same viewing conditions. It is a dimensionless number between 0 (for a perfect reflector) and 1 (for a perfect emitter).

To simplify the above definition, emissivity is a ratio of the thermal radiation emitted by an object compared to a perfect blackbody (ε =1.0). Furthermore, the comparison should be made at the same temperature, wavelength, and viewing conditions.

In context to this guide, consider the emissivity of a blackbody calibrator surface used to perform infrared thermometer and pyrometer calibrations.

 
 

Sakuma-Hattori Equation

The Sakuma–Hattori equation is a mathematical formula for predicting the amount of thermal radiation, radiometric flux or radiometric power emitted from a blackbody or received by a thermal radiation detector.

In 2008, the BIPM CCT-WG5 (i.e. the radiation thermometry working group) recommended the Planckian form of the equation should be used to calibrate (or estimate emissivity uncertainty) for radiation thermometry below 961.8°C (i.e. silver point).

For infrared thermometers with wavelengths between 8 to 14 µm, the following equation and coefficients were recommended for temperatures between -40°C and 500°C.

 
Be careful following ASTM E2758 and E2847. They both claim the formula and coefficients given below work for temperatures between -50°C to 1000°C. However, this is a mistake (as you can see in the above image).

Below, you will see the Sakuma–Hattori formula and coefficients for the IR temperature range with wavelengths between 8 to 14 µm.

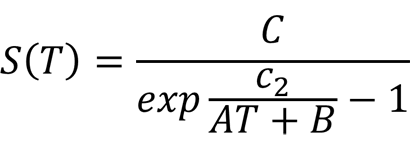
Where:
A – constant 9.364 µm for the 8 to 14 µm band
B – constant 178.4 µm for the 8 to 14 µm band
C – constant 1.0 µm for the 8 to 14 µm band
C₂ – constant: 14387.752 µm · K
T – temperature (K)
S(T) – radiometric signal

Remember this equation. You will use it in the next section to evaluate emissivity uncertainty.

 
 

How to Calculate Emissivity Uncertainty

Calculating emissivity uncertainty is not simple. It requires a series of calculations that are:

1. difficult for most people, and
2. poorly explained by many experts and standards documents.

In my opinion, the ASTM E2847 and E2758 do a terrible job of explaining how to perform the calculation.

Because of this, many people struggle to estimate emissivity uncertainty for their blackbody calibrators and IR thermometers.

In this section, I am going to try to simplify the calculation of emissivity uncertainty by breaking down the process into easy to follow steps.

Overall, the process consists of the following steps:

1. Specify the Measurement Parameters
2. Calculate the S(T) of the Blackbody Source
3. Calculate the S(T) of the Reflected Temperature
4. Calculate the Emissivity Uncertainty
5. Convert Emissivity Uncertainty to Temperature

In each step, you will get additional instructions and information to help you complete the process.

However, if you have a difficult time trying to perform this calculation, just download our Emissivity Uncertainty Calculator. It will automatically perform all of the calculations for you.

Click here to buy the
Emissivity Uncertainty Calculator

 
Now, let’s begin.

 
 

1. Specify the Measurement Parameters

To calculate uncertainty dues to emissivity, first you need to specify the measurement parameters. These include:

• Surface temperature,
• Ambient temperature,
• Emissivity of the surface,
• Emissivity of the instrument, and
• An estimate of emissivity uncertainty

 
 

1.1. Specify the Surface Temperature (typically a blackbody source)

In this step, you will specify the temperature of the surface that you are measuring. Typically, this is the surface or cavity temperature of a blackbody calibrator.

Therefore, indicate the surface temperature of the blackbody source (e.g. 500 °C).

 
 

1.2. Specify the Reflected Temperature (typically the ambient temperature)

Next, specify the reflected temperature. This is commonly the ambient temperature of the environment where the measurement is performed.

Therefore, indicate the ambient temperature of the environment (e.g. 23 °C).

 
 

1.3. Specify the Emissivity of the Surface

Now, find the emissivity of the blackbody surface that will be measured. Typically, the value will range between 0.94 and 0.995. You should be able to find this value in the manufacturer’s manual or datasheet.

In the image below, you will see the nominal emissivity of the Fluke 4180 and 4181 blackbody calibrators listed in the manufacturer’s datasheet.

 
 

1.4. Specify the Emissivity of the Instrument

Next, find the emissivity of the instrument (e.g. IR Thermometer or Pyrometer) used to measure the blackbody surface. Typically, the value will range between 0.9 and 1.0.

You should be able to find this value in the instrument settings menu. Otherwise, you may need to refer to the manufacturer’s manual or datasheet.

TIP: Some instruments can be adjusted to match the emissivity of the source in order to reduce emissivity uncertainty and errors.

 
In the image below, you will see an excerpt from the Fluke 62 MAX IR Thermometer user guide showing you how to adjust the emissivity setting.

 
 

1.5. Specify the Estimated Emissivity Uncertainty (typically 0.01 to 0.02)

Finally, estimate the value for emissivity uncertainty. Typically, the value ranges between 0.01 and 0.02. Many papers and application notes published by Fluke Calibration suggest an emissivity uncertainty of 1% of value. Therefore, an emissivity value of 0.95 would have an uncertainty of 0.0095 (i.e. 0.95 x 0.01 = 0.0095).

In the image below, you will see a graph (made by Fluke) that charts the effects of a 1% emissivity error vs temperature

 
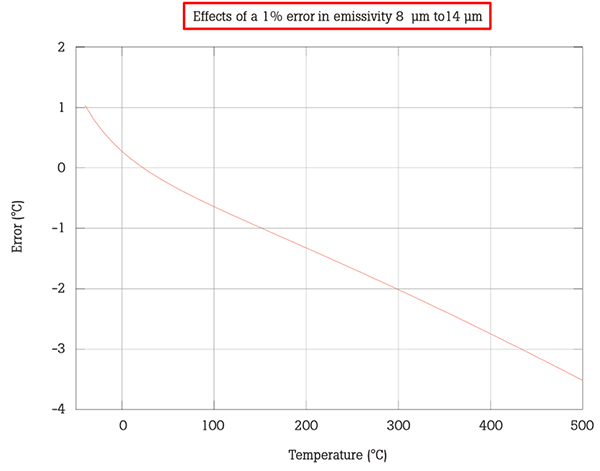
Alternatively, other documents suggest emissivity uncertainty values ranging from 0.01 to 0.02. In fact, ASTM E2847 gives an example that includes an expanded uncertainty of 0.02 for the emissivity of a blackbody surface.

 
 

2. Calculate the S(T) of the Blackbody Source Using the Sakuma-Hatori Equation

Now that step 1 is complete, calculate the radiometric value S(T) for the blackbody source temperature.

 
 

2.1. Convert the Blackbody Temperature to Kelvin

First, convert your blackbody temperature to Kelvin.

If your temperature is in degrees Celsius, then convert your temperature to Kelvin by following the instructions below:

1. Add 273.15 to the temperature value.

 
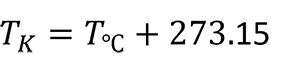
If your temperature is in degrees Fahrenheit, then convert your temperature to Kelvin by following the instructions below:

1. Add 459.67 to the temperature value,
2. Multiply the result of Step 1 by 5,
3. Divide the result of Step 2 by 9.

 
 

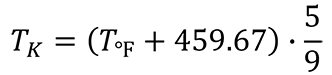
2.2 Calculate the Radiometric Value S(T) for the Black Body Source

Next, use the Sakuma-Hatori equation to calculate the radiometric value S(T) for the blackbody source. You will need the values for constants A, B, C, and c2. These can be found at the beginning of this guide.

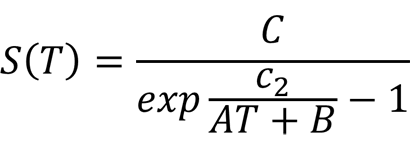
To calculate the radiometric value S(T), follow the steps below. They are given in the order of operations to calculate the result.

1. Multiply constant A by the temperature in Kelvin.
2. Add constant B to the result from Step 1.
3. Divide constant c2 by the result from Step 2.
4. Use the exponential function to raise e to the power of the result from Step 3.
5. Subtract one (i.e. 1) from the result of Step 4.
6. Finally, divide constant C by the result of Step 5.

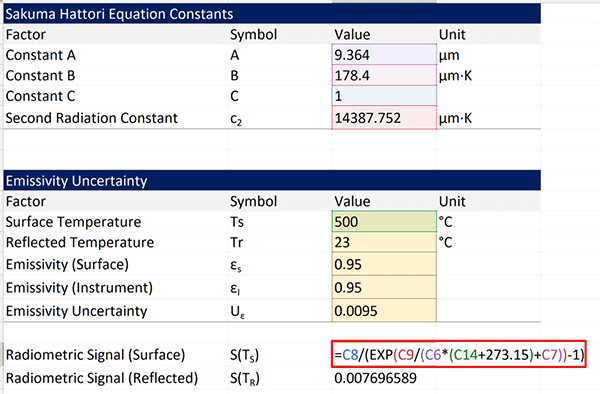
In the image below, you will see how this calculation is performed in Microsoft Excel. If you look at the function in the red rectangle, you will find the formula that matches the instructions above.

 
 

3. Calculate the S(T) of the Reflected Temperature Using the Sakuma-Hatori Equation.

Now that step 2 is complete, calculate the radiometric value S(T) for the reflected temperature. This will be the ambient temperature of the environment.

 
 

3.1. Convert the Reflected Temperature to Kelvin

Similar to Step 2.1, convert the reflected temperature (i.e. ambient temperature) to Kelvin.

 
 

3.2 Calculate the Radiometric Signal S(T) for the Reflected Temperature

Next, use the Sakuma-Hatori equation to calculate the radiometric value S(T) for the reflected temperature. Similar to the Step 2.2, you will need the values for constants A, B, C, and c2 that can be found at this beginning of this guide.

Now, calculate the radiometric value S(T) following the steps below. They are given in the order of operations to calculate the result.

1. Multiply constant A by the temperature in Kelvin.
2. Add constant B to the result from Step 1.
3. Divide constant c2 by the result from Step 2.
4. Use the exponential function to raise e to the power of the result from Step 3.
5. Subtract one (i.e. 1) from the result of Step 4.
6. Finally, divide constant C by the result of Step 5.

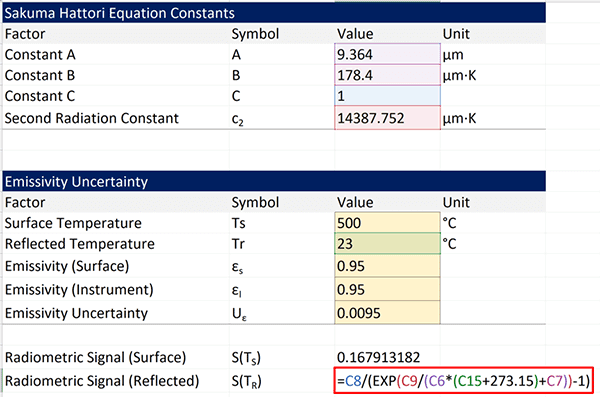
In the image below, you will see how this calculation is performed in Microsoft Excel. If you look at the function in the red rectangle, you will find the formula that matches the instructions above.

 
 

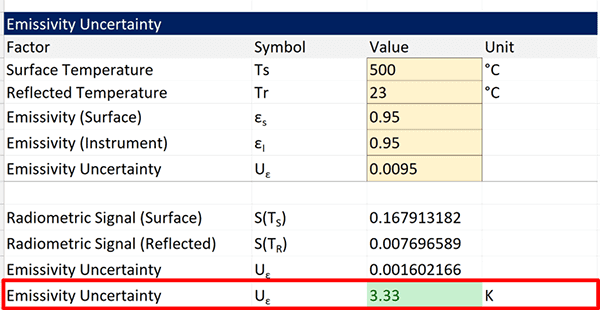
4. Calculate the Emissivity Uncertainty

Now that you have the calculated radiometric signals S(T) for your blackbody source and ambient temperature, you can calculate the uncertainty due to emissivity.

Below, you will see the formula recommended by ASTM E2847.

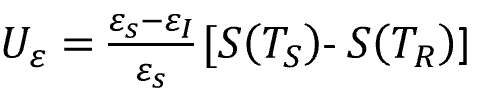
Where,
U_ε = emissivity uncertainty
ε_S = emissivity of the source
ε_I = emissivity of the instrument
S(T_S) = radiometric signal of the source temperature
S(T_R) = radiometric signal of the reflected temperature

To calculate the uncertainty due to emissivity, follow the instructions below. They are in order of mathematical operations.

1. Subtract the source emissivity by the instrument emissivity.
2. Divide the result of Step 1 by the instrument emissivity.
3. Subtract the radiometric signal of the source by the radiometric signal of the reflected temperature.
4. Multiply the result of Step 2 by the result of Step 3.

The result is the emissivity uncertainty. However, it is a radiometric signal. So, you have to convert it to temperature units to add it to your uncertainty budgets.

 
 

5. Convert Emissivity Uncertainty to Temperature

Finally, convert emissivity uncertainty radiometric signal to temperature in Kelvin. To do this, you will need to use the Sakuma-Hatori equation and solve for temperature.

This requires working the steps of the equation backwards to solve for temperature.

I have already done this for you. Look at the equation below. It is the equation to convert emissivity uncertainty to temperature in Kelvin. Fluke Calibration has published a similar equation in some of their application notes and infographics. However, their formula has a mistake in it. Use the formula below instead.

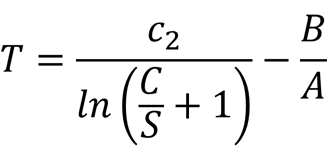
To convert the emissivity uncertainty to temperature in Kelvin, follow the instructions below. They are in order of mathematical operations.

1. Divide constant C by the radiometric signal for emissivity uncertainty.
2. Add one (i.e. 1) to the result of Step 1.
3. Calculate the natural logarithm of the result of Step 2.
4. Divide constant c2 by the result of Step 3.
5. Divide constant B by constant A.
6. Subtract the result of Step 4 by the result of Step 5.

When finished, you will have emissivity uncertainty in Kelvin which is equivalent to degrees Celsius.

 
 

Resources for Emissivity Uncertainty

To evaluate uncertainty due to emissivity, it is good to have professional or scholarly resources to support your evaluations. In this section, you will see three great resources to support this guide and your calculations of emissivity uncertainty.

 
 

ASTM E2758

The ASTM E2758 is the most recommended method to evaluate emissivity uncertainties. It is referenced in more papers and documents than any other method. So, if you want a copy of the most referred resource, go to the ASTM website and purchase one for yourself.

 
 

ASTM E2847

The ASTM E2847 is an alternative resource to ASTM E2758. It is not referenced or recommended as much, but it contains the same information. Additionally, it is a standard calibration method which may be beneficial if you are a calibration laboratory. You will get a calibration method (that does not need validation) and information on how to evaluate emissivity uncertainty.

 
 

Fluke Application Note 4276605A_EN

Need a free resource? Download this application note from Fluke Calibration. It covers the same methodology in this guide to help you correct your IR temperature measurements for errors caused by emissivity.

Regardless of what your assessor may say, you can use this method. It is based on ASTM E2758 and does not only apply to Fluke 4180 and 4181 infrared calibrators.

To back up my previous statement, you can see the references from the application note in the image below. It clearly gives a reference to ASTM E2758.

 
 

Conclusion

Emissivity uncertainty is a significant contributor to measurement uncertainty for infrared thermometer and pyrometer calibrations and measurements. Most accreditation bodies require laboratories to include emissivity in their uncertainty budgets. Even when it is not required, many assessors know it is a significant contributor and check to see if you included it in your uncertainty analysis.

As a result, this has led to an increase in the number of deficiencies cited in relation to emissivity missing in uncertainty budgets.

In this guide, you should have learned:

1. What is the definition of emissivity?
2. What is the Sakuma Hatori equation,
3. How to calculate emissivity uncertainty or correction.

With this information, you should be able to evaluate emissivity uncertainty for your infrared temperature uncertainty budgets. Give it a try and let me know if this guide has helped you.

If you do not want to make your own calculator, you can buy ours by clicking the button below.

 
Click here to download the
ISOBudgets Emissivity Uncertainty Calculator