Collecting Data
The number of samples collected during experimentation has an effect on the analysis of results and the validity of the test data collected. Over the years, I have observed several conflicting accounts of how many samples one should collect during experimentation. According to many introductory statistics textbooks, the number of samples collected depends on the population. A small population is considered a collection of 30 samples or less, while a large population is considered a collection of more than 30 samples. However, more advanced subject areas of statistics will have multiple assertions in relation to the goals of analysis and the expected confidence in results. If you were to survey a group of professionals from different organizations and different industries, you would receive a collection of varied opinions. This is the result of differing world views; each person and organization is going to have different goals. Therefore, they will have a degree of varied opinions.
What To Do
In my professional opinion, the number of samples you collect should be in relation to your organization’s goals and the level of confidence expected in the results. If your laboratory seeks to attain a 95.45% level of confidence (where k=2.00), I recommend that you collect 22 samples for each experiment. If your goal was to achieve a confidence level of 99%, I would recommend that you collect 100 samples. Why? The answer is outliers. You can validate your results with outliers. If you collect 22 samples and seek to achieve a 95.45% level of confidence, you will typically find one outlier in your pool of collected samples. This is how you can ensure that you are achieving the level of confidence that meets your goals. Furthermore, it allows you to control the effectiveness and efficiency of your data collection efforts. Why collect 100 samples if you only need 22; or, why collect 22 samples if you need 100. Only expend the resources that you need to achieve your goals. Otherwise, you are wasting your time and resources that could be used to perform other tasks. Using the following equation, you can determine the appropriate number of samples you wish to collect in order to achieve a specific level of confidence. 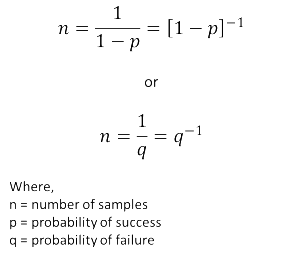
Let’s Break It Down
Not sure if my theory is valid. Then, let me show you quantitative and qualitative results that support my opinion. Using a Monte Carlo simulation, I will generate a pool of random data that is supposed to conform to a specified level of confidence (i.e. 95.45%) exhibiting a Gaussian distribution. With this data, I will calculate the mean, standard deviation, and degrees of freedom and report the results for you to evaluate. From here, you can formulate your own opinion and chose to agree or disagree with me.
The Results
95.46% of trials exhibited one outlier or less
68.18% of trials exhibited at least one outlier
4.54% of trials exhibited more than one outlier
Notes
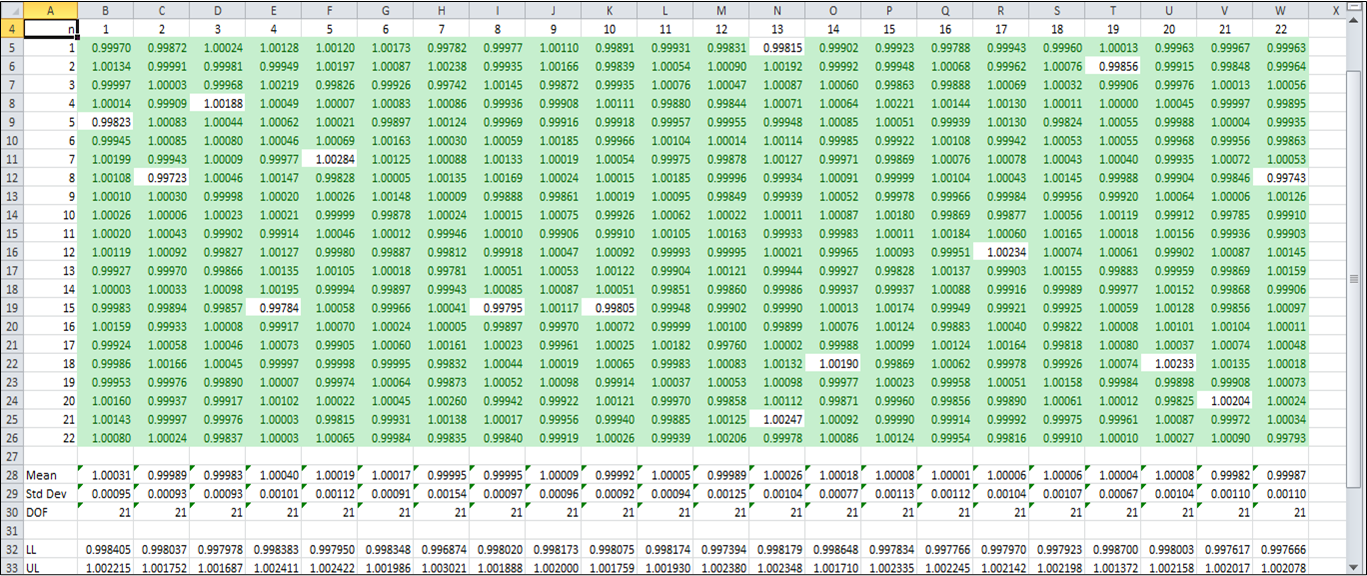
1| The numbers in the left column represent the sample number for each trial, totaling 22.
2| The numbers in the top row represent the trial number, totaling 22.
3| The upper and lower limits were quantified by calculating the sum and the difference of the mean and twice the standard deviation (i.e. 2-sigma).
4| The values that do not conform, or outliers, are the cells not highlighted in green.
5| Click the image to make it larger
Now that I have provided you some information and methods that you can use to determine the most efficient number of samples to collect for your repeatability experiments, how many samples will you collect?