How to Calculate Standard Uncertainty

Short answer: The two most common methods to calculate standard uncertainty are 1) calculate the standard deviation from a Type A uncertainty evaluation, or 2) convert an expanded uncertainty to a standard uncertainty.

There are a few ways to calculate standard uncertainty. The two most common methods are:

Calculate the standard deviation from a Type A uncertainty evaluation
Conversion from expanded uncertainty to standard uncertainty

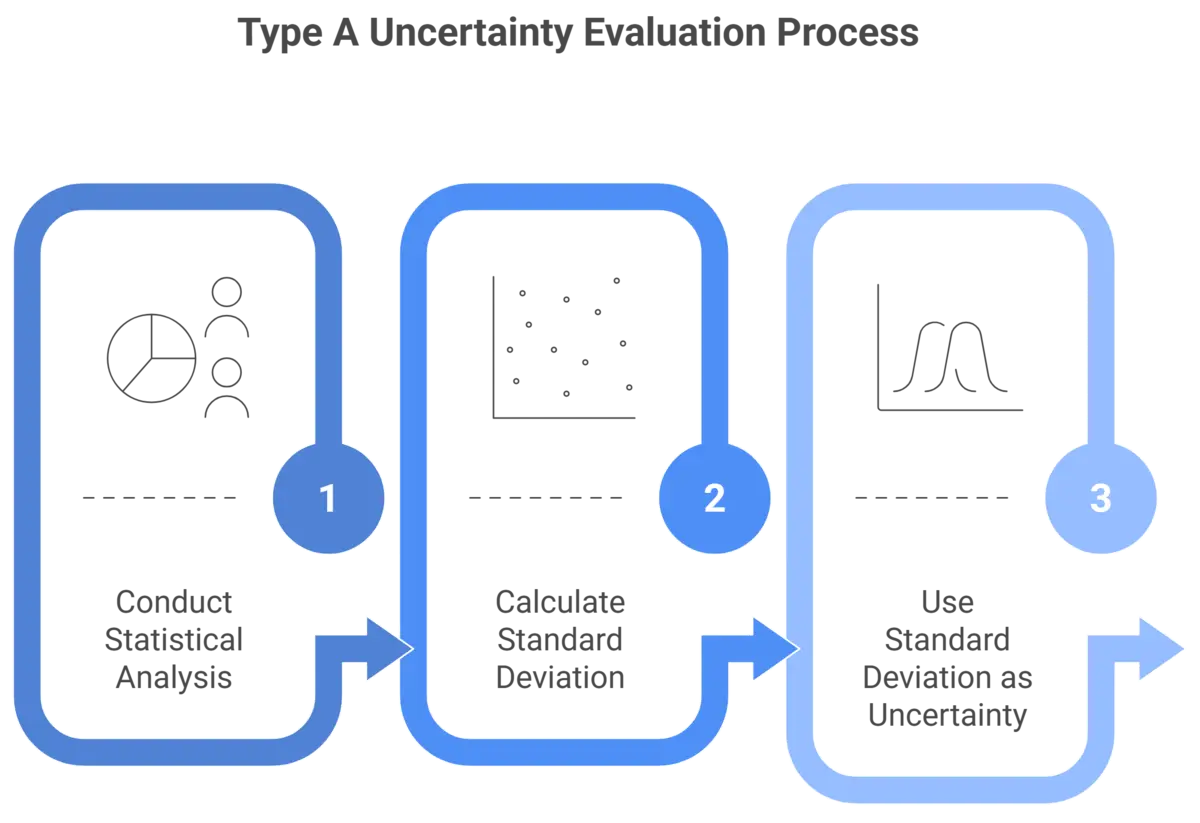
Method 1: Type A Uncertainty Evaluation

Evaluate uncertainty from Type A evaluations using analysis of variance (ANOVA) or other statistical methods. Most Type A evaluations result in a standard deviation (68 % level of confidence, where k=1) that may be used as a standard uncertainty – no further conversion needed.

Calculate Standard Deviation as the Standard Uncertainty Diagram

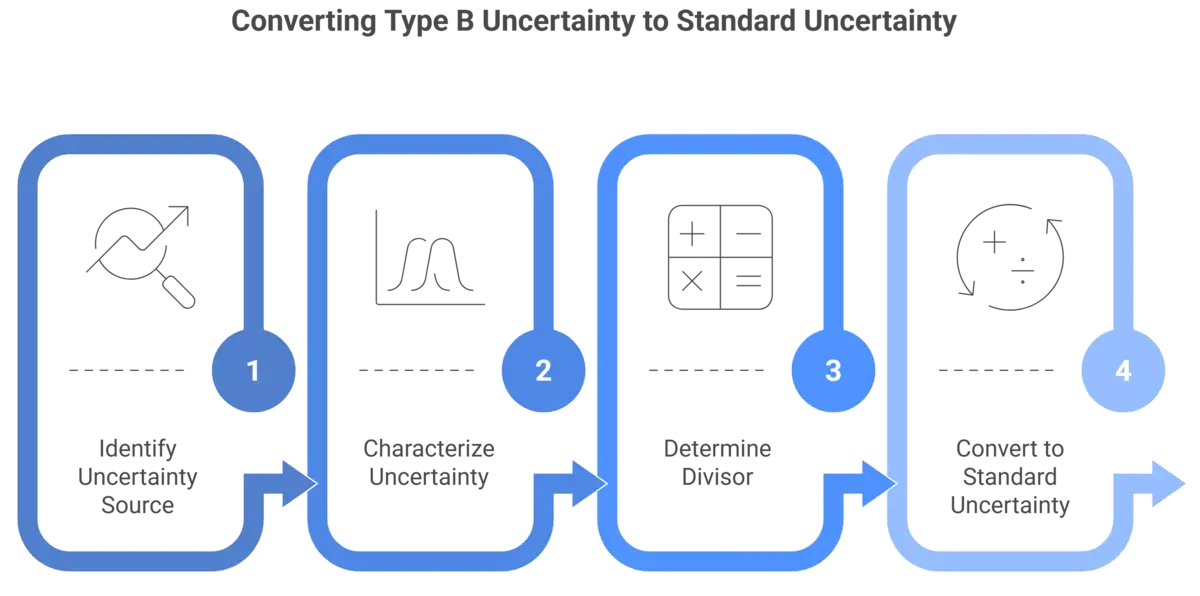
Method 2: Conversion to Standard Uncertainty

Some uncertainties, typically Type B uncertainties, need to be converted to a standard uncertainty (i.e standard deviation or standard deviation equivalent). Step-by-step instructions to convert these uncertainties is given below.

Identify and quantify a source of uncertainty.
Characterize the uncertainty – assign a probability distribution.
Determine the divisor associated with the probability distribution.
Convert to standard uncertainty – divide the uncertainty by the divisor

Convert Uncertainty to Standard Uncertainty Diagram

FAQ

What is standard uncertainty?

Measurement uncertainty expressed as a standard deviation with a 68.27 % level of confidence.

According to the Vocabulary in Metrology (VIM), standard measurement uncertainty is defined as “measurement uncertainty expressed as a standard deviation.”

How to convert to standard uncertainty?

Where applicable, convert expanded uncertainties to a standard uncertainty following the instructions below.

Identify and quantify a source of uncertainty.
Characterize the uncertainty – assign a probability distribution.
Determine the divisor associated with the probability distribution.
Convert to standard uncertainty – divide the uncertainty by the divisor

How to convert standard deviation to standard uncertainty?

Typically, a standard deviation does not need to be converted to a standard uncertainty because it is already expressed at a 68.27 % level of confidence. Otherwise, a standard deviation can be divided by a coverage factor of one, but this is typically meaningless.

What are examples of standard uncertainty?

Below, are some common examples of standard uncertainty.

Example 1: Repeatability and Reproducibility

Repeatability and reproducibility evaluations conducted in accordance with ISO 5725-2 and ISO 5725-3 will produce standard deviations that can be used as standard uncertainties.

Example 2: Drift Specification

Manufacturer drift specifications are typically considered an expanded uncertainty. They can be characterized with one of the following distributions:

Normal distribution,
Rectangular distribution, or
Triangle distribution.

Based on the assigned distribution, the specification will be converted to a standard uncertainty by dividing its value by a divisor.

The specification will be converted to a standard uncertainty by dividing its value by a divisor associated with the assigned probability distribution.

Example 3: Calibration Uncertainty

Uncertainties from a calibration report are typically expressed to a 95 % confidence interval where k=2. The uncertainty is converted to a standard uncertainty by dividing it by its coverage factor k (i.e. 2).

Example 4: Instrument Resolution

Instrument resolutions are commonly characterized by a rectangular or half-rectangular distribution. The resolution value is converted to a standard uncertainty by dividing the resolution by an appropriate divisor (e.g. √3 or 2√3).

What is the difference between standard uncertainty and expanded uncertainty?

Standard uncertainty is a measurement uncertainty that has the same level of confidence as a standard deviation (e.g. 68.27 % C.I.).

An expanded uncertainty is a standard uncertainty multiplied by a coverage factor greater than one, so it has a level of confidence greater than a standard uncertainty (e.g. 95.45 % C.I.). However, expanded uncertainties can be expressed at other levels of confidence (e.g. 99 %, 99.73 %, or 100 % C.I.).

What is the difference between standard deviation and standard uncertainty?

A standard deviation can be a standard uncertainty, but a standard uncertainty may not be a standard deviation. Instead, it may be a standard deviation equivalent.

Typically, a standard deviation is determined using statistical techniques associated with Type A uncertainty evaluations.

However, a standard uncertainty can be determined with a Type B uncertainty evaluation where it may be converted from an expanded uncertainty to a standard deviation equivalent.

Sometimes, these conversions produce a standard deviation (e.g an expanded uncertainty with a Normal distribution where it is a multiple of a standard deviation per JCGM 100:2008 section 4.3.3).

Otherwise, the conversion results in a standard deviation equivalent (e.g. an uncertainty with a rectangular distribution divided by the square root of three per JCGM 100:2008 section 4.3.7).

Glossary

Standard Measurement Uncertainty: measurement uncertainty expressed as a standard deviation. (Source: JCGM 200:2012, 2.30)
Standard Deviation: a statistical measure quantifying the dispersion or spread (variation) of data points in a dataset relative to the mean (average), indicating how closely values cluster around the average
Expanded Measurement Uncertainty: the product of a combined standard measurement uncertainty and a factor larger than the number one. (Source: JCGM 200:2012, 2.35)
Combined Standard Measurement Uncertainty: standard measurement uncertainty that is obtained using the individual standard measurement uncertainties associated with the input quantities in a measurement model. (Source: JCGM 200:2012, 2.31)
Coverage Factor: number larger than one by which a combined standard measurement uncertainty is multiplied to obtain an expanded measurement uncertainty. (Source: JCGM 200:2012, 2.38)
Type A Evaluation of Measurement Uncertainty: evaluation of a component of measurement uncertainty by a statistical analysis of measured quantity values obtained under defined measurement conditions. (Source: JCGM 200:2012, 2.28)
Type B Evaluation of Measurement Uncertainty: evaluation of a component of measurement uncertainty determined by means other than a Type A evaluation of measurement uncertainty. (Source: JCGM 200:2012, 2.29)
Measurement Repeatability: measurement precision under a set of repeatability conditions of measurement (Source: JCGM 200:2012, 2.21)
Measurement Reproducibility: measurement precision under reproducibility conditions of measurement (Source: JCGM 200:2012, 2.25)
Instrumental Drift: continuous or incremental change over time in indication, due to changes in metrological properties of a measuring instrument (Source: JCGM 200:2012, 4.21)
Instrumental Bias: average of replicate indications minus a reference quantity value (Source: JCGM 200:2012, 4.20)
Resolution: smallest change in a quantity being measured that causes a perceptible change in the corresponding indication (Source: JCGM 200:2012, 4.14)
Level of Confidence: the likelihood that a set of measurement values are contained within a specified coverage interval. (Source: JCGM 200:2012, 2.37)