Combined Uncertainty Formulas from the JCGM 100:2008
The Guide to the Expression of Uncertainty in Measurement (GUM) or JCGM 100:2008 provides two main formulas for calculating the combined standard uncertainty.
Uncorrelated Input Quantities
In section 5.1 of the JCGM 100:2008, the GUM gives a formula for calculating the combined standard uncertainty where all input quantities are independent or orthogonal. (This is the most commonly used)
uc2(y) = Σ(δf/δxi)2·u2(xi)
The combined standard measurement uncertainty formula from the JCGM 100:2008 (GUM), section 5.1 is provided below.
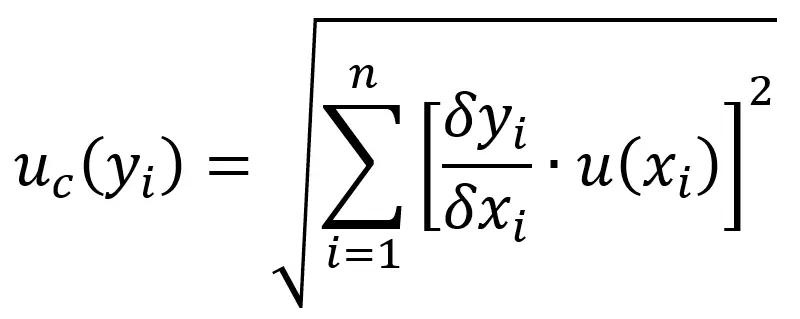
Correlated Input Quantities
In section 5.2 of the JCGM 100:2008, the GUM gives a formula for calculating the combined standard uncertainty where two or more input quantities are interdependent or correlated.
uc2(y) = ΣiΣj(δf/δxi)·(δf/δxj)·u(xi,xj)
The combined standard measurement uncertainty formula from the JCGM 100:2008 (GUM), section 5.2 is provided below.
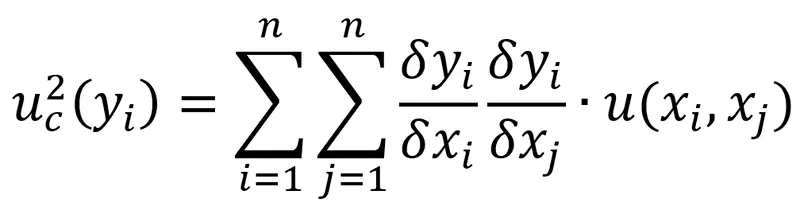
Combined Uncertainty Formula – Common Variations
There are several variations of the formula to calculate combined standard uncertainty. The simplest is the formula that uses the RSS method to combine uncertainties when all input values are the same unit of measurement and level of magnitude. Otherwise, variations exist to include the use of sensitivity coefficients or relative uncertainties.
An example of each is given below.
Simple Formula to Combine Uncertainties
This formula is used to calculate the combined standard uncertainty when all input quantities have the same unit of measurement, same level of magnitude, and a sensitivity coefficient equal to one.
uc = √(u12 + u22 + ui2)
Where,
uc – combined standard uncertainty
ui – standard uncertainty of the input quantity
Formula to Combine Uncertainties with Sensitivity Coefficients
This formula is used to calculate the combined standard uncertainty when input quantities have the different units of measurement, different levels of magnitude, and(or) a sensitivity coefficient not equal to one.
uc = √(c1·u12 + c2·u22 + ci·ui2)
Where,
uc – combined standard uncertainty
ui – standard uncertainty of the input quantity
ci – sensitivity coefficient
Expanded Formula to Combine Uncertainties with Sensitivity Coefficients
This formula is an expanded version of the previous formula. It is used when sensitivity coefficients have not yet been calculated, so the input quantities can be converted at the time of the combined uncertainty evaluation.
uc = √[(δy1/δx1)·u12 + (δy2/δx2)·u22 + (δyi/δxi)·ui2]
Where,
uc – combined standard uncertainty
ui – standard uncertainty of the input quantity
δyi – change or difference in the result associated with the change in the input quantity
δxi – change or difference in the input quantity
Formula to Combine Uncertainties with Relative Uncertainties
This formula is used to calculate the combined standard uncertainty when relative uncertainties are appropriate (according to uncertainty propagation rules) and the intent is to evaluate relative uncertainties.
uc = √[(ux1/x1)2 + (ux2/x2)2 + (uxi/xi)2]
Where,
uc – combined standard uncertainty
uxi – standard uncertainty of the input quantity
xi – value of the input quantity
Frequently Asked Questions (FAQ)
What is the combined uncertainty?
The combined uncertainty is the result (i.e. standard uncertainty) of combining individual standard uncertainties using the RSS method.
According to the Vocabulary in Metrology (VIM), combined uncertainty is the “standard measurement uncertainty that is obtained using the individual standard measurement uncertainties associated with the input quantities in a measurement model.”
How to calculate the combined uncertainty?
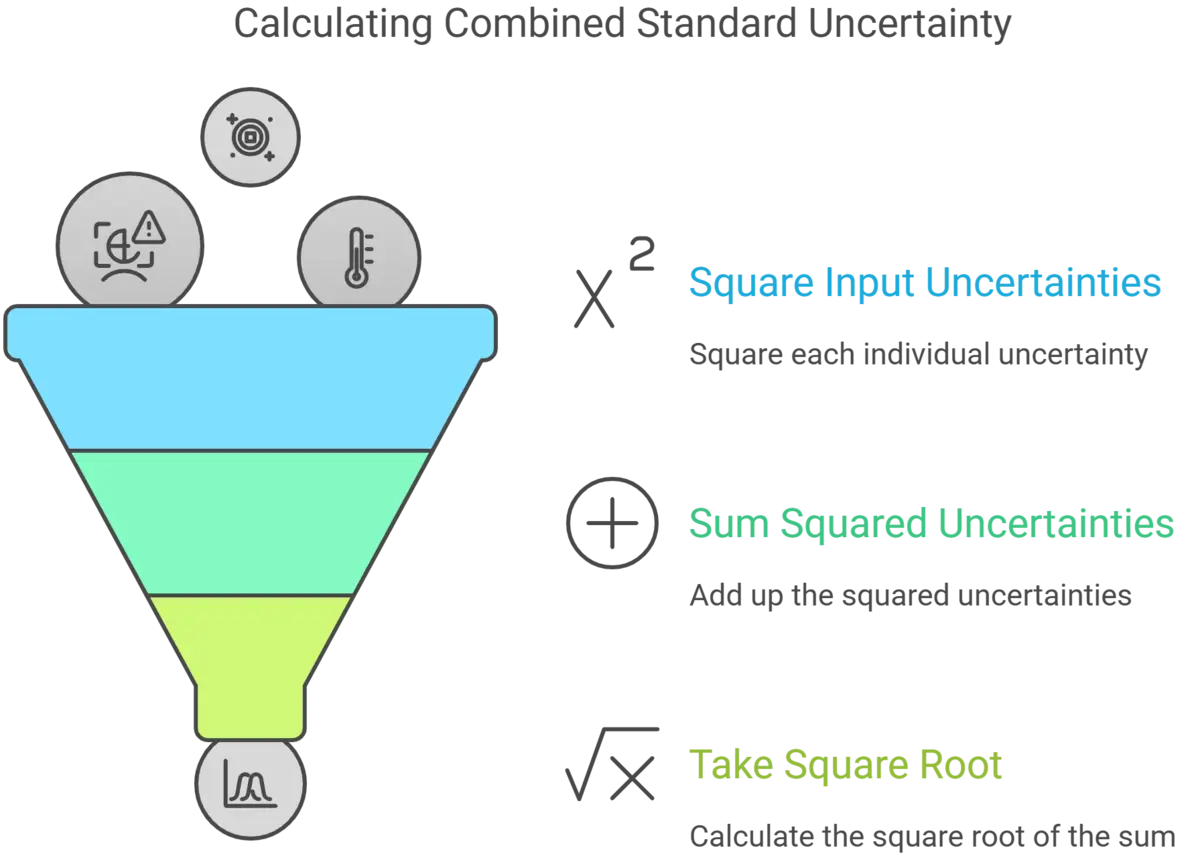
Calculate the combined standard uncertainty using the RSS method. Step-by-step instructions are provided below:
- Identify and Quantify Uncertainty – Find significant sources of uncertainty and determine their magnitude.
- Characterize Uncertainty – Assign a probability distribution to each source of uncertainty.
- Convert to Standard Uncertainty – Divide each uncertainty by the divisor associated with its probability distribution.
- Convert to Variance – Square each standard uncertainty.
- Calculate the Combined Variance – Add together all the squared standard uncertainties (i.e. variances).
- Calculate the Combined Uncertainty – Calculate the square root of the combined variance
How to combine percentage uncertainties?
Percentage uncertainties (i.e. relative uncertainties) are combined in the same manner as absolute uncertainties. First, characterize each uncertainty by assigning an appropriate probability distribution. Next, convert each percentage uncertainty to a standard uncertainty (i.e. standard deviation equivalent). Finally, combined the uncertainties using the RSS method.
The combined standard uncertainty will be a percentage. Typically, relative to the measurand and expressed as a percentage of reading, indicated value, or other similar term.
What is the RSS method of uncertainty?
The RSS method stands for the square root of the sum of squares method.
It is the method used to calculate the combined standard measurement uncertainty, where each standard uncertainty is squared and added together. Then, the square root is calculated from the sum of squared uncertainties.
According to the JCGM 100:2008, it is actually defined as the square root of the total combined variance.
How do you combine multiple sources to get the combined standard uncertainty?
Convert each source of uncertainty to a standard uncertainty (i.e. standard deviation) and combine them using the square root of the sum of squares formula (known as the RSS method) per section 5 of the JCGM 100:2008.
According to the JCGM 100:2008 section 5.1.2, the “combined standard uncertainty is the positive square root of the combined variance (i.e. sum of squared standard deviations)”.
How to combine uncertainties of different units?
Use sensitivity coefficients or relative uncertainties to combine uncertainties with different units of measurement.
Method #1: Sensitivity Coefficients
First, you can use sensitivity coefficients. Sensitivity coefficients can be used to convert uncertainties to the same unit of measurement as the result or measurand. Then, the converted values can be combined using the RSS method.
This makes sensitivity coefficients ideal for calculating the combined standard uncertainty. Plus, they work for any scenario. However, determining sensitivity coefficients can require experimentation or complex evaluations that some people may find difficult.
Method #2: Relative Uncertainties
Otherwise, you can use relative uncertainties. For simple formulas, you can convert the uncertainties to terms relative to the measurand (i.e. percentage or parts per million equivalent). Then, the relative terms can be combined using the RSS method.
This method is popular because it is easy to implement. However, it is not applicable for all scenarios (typically, complex formulas). The rules for the propagation of uncertainty should be carefully followed to avoid errors in estimated uncertainties.
Glossary
- Measurement Uncertainty
- non-negative parameter characterizing the dispersion of the quantity values being attributed to a measurand, based on the information used. (Source: JCGM 200:2012, 2.26)
- Standard Measurement Uncertainty
- measurement uncertainty expressed as a standard deviation. (Source: JCGM 200:2012, 2.30)
- Combined Standard Measurement Uncertainty
- standard measurement uncertainty that is obtained using the individual standard measurement uncertainties associated with the input quantities in a measurement model. (Source: JCGM 200:2012, 2.31)
- Measurand
- quantity intended to be measured. (Source: JCGM 200:2012, 2.3)
- Relative Measurement Uncertainty
- measurement uncertainty expressed in a term relative to the measurand.
- Absolute Measurement Uncertainty
- measurement uncertainty expressed in the same unit of measurement as the measurand.
- Sensitivity Coefficient
- a quotient of the change in an indication of a measuring system and the corresponding change in a value of a quantity being measured. (Source: JCGM 200:2012, 4.12)
- Probability Distribution
- a function or table that describes the likelihood of all possible outcomes for a random variable associated with an experiment or event.