According to the Vocabulary in Metrology (VIM), expanded measurement uncertainty is “the product of a combined standard measurement uncertainty and a factor larger than the number one.” (Source: JCGM 200:2012, 2.35)

Measurement uncertainty is commonly expressed in ISO/IEC 17025 accredited reports and ISO 17034 accredited certificates as an expanded uncertainty.
Typically, the expanded uncertainty is reported to 95.45 % confidence interval using coverage factor (k) of 2. See JCGM 100:2008 table G.1.
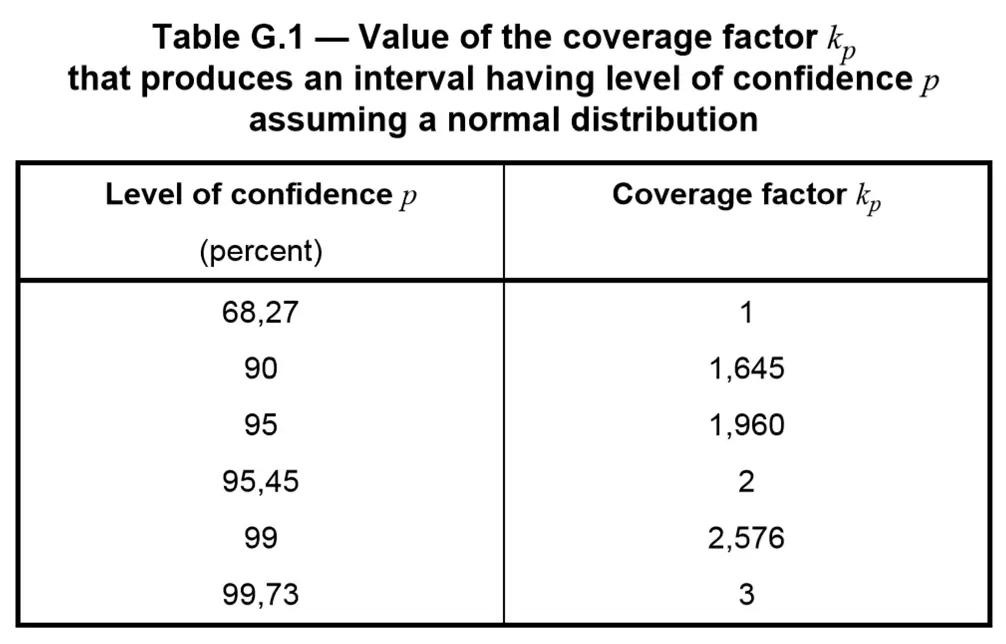
Otherwise, the coverage factor is determined using the Student’s T distribution when the effective degrees of freedom are less than 10. See JCGM 100:2008 section G.6.6.
FAQ
How to calculate expanded uncertainty?
Calculate the expanded uncertainty by multiplying the combined standard uncertainty by a coverage factor associated with a desired level of confidence (e.g. 95 %).
What is Combined Measurement Uncertainty?
Combined standard measurement uncertainty is the result of combining individual standard measurement uncertainties using the square root of the sum of squares (RSS) method.
What is a coverage factor?
A coverage factor is a multiplier larger then one used to expand the combined standard uncertainty to a desired level of confidence (e.g. 95 % confidence where k=2)
What coverage factor is used to calculate expanded uncertainty?
The coverage factor used depends on the following factors:
- desired level of confidence and,
- where appropriate, the effective degrees of freedom.
Specify the desired level of confidence and find the associated coverage factor from JCGM 100:2008 Table G.1. For example, an ISO/IEC 17025 accredited laboratory needs to estimate uncertainty to a 95.45 % level of confidence using a coverage factor of 2 from JCGM 100:2008 Table G.1. The coverage factors in the table are equal to using the t-distribution with infinite degrees of freedom.
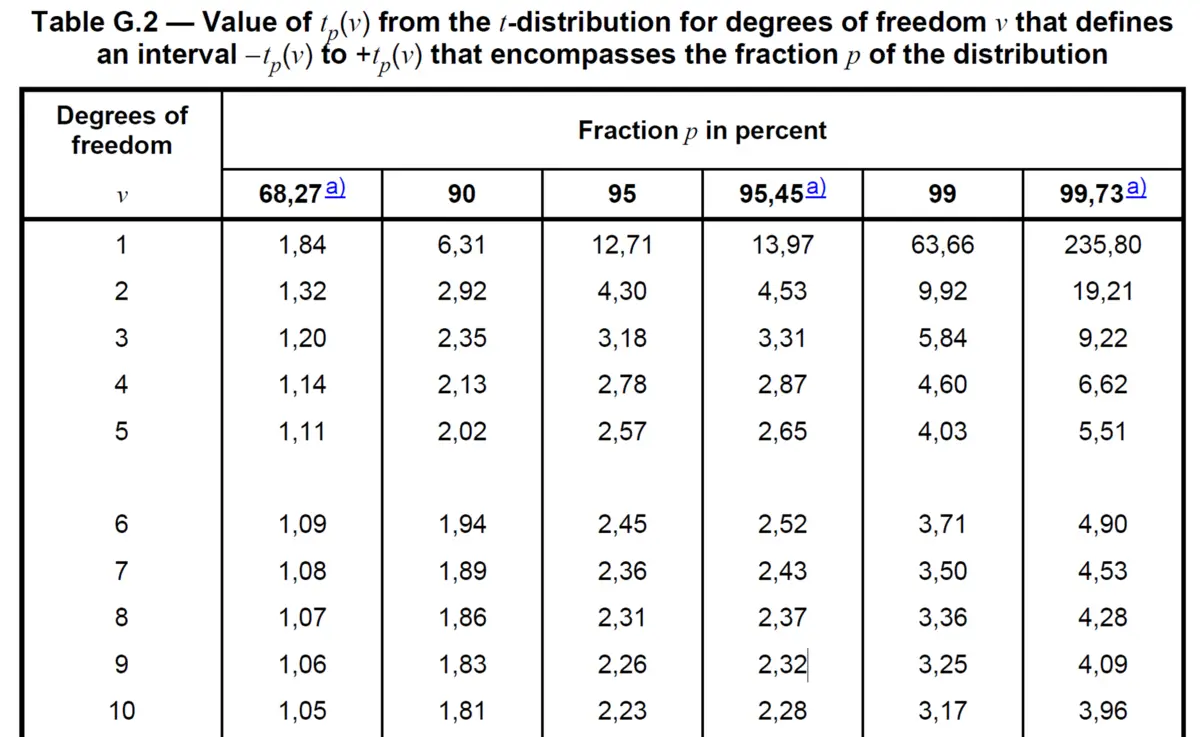
When the effective degrees of freedom are less than 10 (JCGM 100:2008, G.6.6), use the t-distribution or JCGM 100:2008 Table G.2 to find the coverage factor. For example, a combined standard uncertainty with 9 effective degrees of freedom would use a coverage factor of 2.32 according to JCGM 100:2008 Table G.2.
What is level of confidence?
Also known as “coverage probability,” the level of confidence is the likelihood that a set of measurement values are contained within a specified coverage interval.
For example, a 95 % level of confidence would imply that 95 out of 100 measurement values will stay within the coverage interval. Likewise, it would also infer that 1 in 20 measurement values will occur outside the coverage interval.
Glossary
- Expanded Measurement Uncertainty
- the product of a combined standard measurement uncertainty and a factor larger than the number one. (Source: JCGM 200:2012, 2.35)
- Combined Standard Measurement Uncertainty
- standard measurement uncertainty that is obtained using the individual standard measurement uncertainties associated with the input quantities in a measurement model. (Source: JCGM 200:2012, 2.31)
- Coverage Factor
- – number larger than one by which a combined standard measurement uncertainty is multiplied to obtain an expanded measurement uncertainty. (Source: JCGM 200:2012, 2.38)
- Effective Degrees of Freedom
- the degrees of freedom of the combined standard measurement uncertainty (uc) obtained from the Welch-Satterthwaite formula and used to determine the coverage factor (k) approximated by a t-distribution. (Source: JCGM 100:2008, G.4)
- Level of Confidence
- the likelihood that a set of measurement values are contained within a specified coverage interval. (Source: JCGM 200:2012, 2.37)