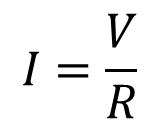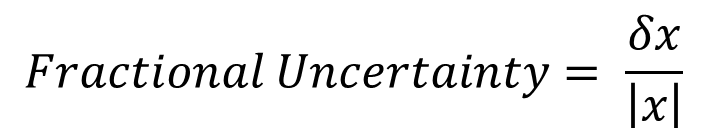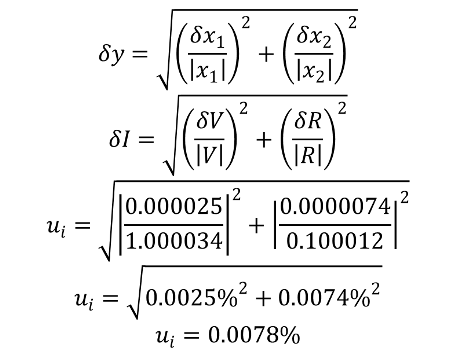Propagation of uncertainty is an important aspect of uncertainty analysis. It is a method that transmits the uncertainties of independent variables through an equation to estimate the uncertainty of the final calculation. Commonly practiced in error and uncertainty analysis, the method is useful for estimating uncertainty where physical quantities cannot be measured directly.
Indirect Measurements
Many physical quantities cannot be measured with a single direct measurement. Instead, the quantity is the calculated result, using an equation, where direct measurements were performed to determine the value of two independent variables. For example, the value of current can be calculated using the Ohm’s Law equation where current is the calculated quotient of voltage over resistance.
Identify the Equation
Before making indirect measurements, it is a good idea to identify the equation that will be used to calculate your final result. If you are not a physicist or an engineer, it is always helpful to have a good physics textbook on hand for reference.
For this example, we will look at the Ohm’s Law equation for solving the value of current where the values for voltage and resistance can be quantified.
Quantify the Measurement Result
Now that we have identified an equation, the next task will be to quantify the independent variables. To accomplish this, we must quantify the value of the resistor (R) used in series with the circuit and the value of the voltage drop (V) across the resistor measured using a digital multimeter. Once we have measured or quantified the independent variables for voltage (V) and resistance (R), we can calculate the value of current (I).
For our example, we will assign the following values for the variables V and R. I is calculated using the Ohm’s Law equation.
V = 1.000034
R = 0.100012
I = 9.999140
Estimate the Uncertainty
Similar to most measurement results, it is common practice to estimate the uncertainty associated with each measurement result. This can be accomplished by the combining the uncertainty contributors relevant with the measurement(s) performed, which may include, but are not limited to the Calibration Measurement Capability (CMC) statement in your scope of accreditation, the resolution of the standard, the resolution of the Unit Under Test (UUT), the repeatability of the measurement results, and(or) other influences that impact the measurement result. If you are unfamiliar with the information expressed in this paragraph, I recommend that you refer to the “Guide to the Expression of Uncertainty in Measurement.”
Below, I have assigned two values for the estimated uncertainty associated with each measurement result.
V = 0.000025 V
R = 0.0000074 Ohm
Calculate Fractional Uncertainty
Since our goal is to propagate uncertainty where we have values with different units of measure, we will look into calculating fractional uncertainty. Fractional uncertainty is a dimensionless quantity relative to the percentage of the uncertainty associated with the measurement result. Hence, calculate the percentage of uncertainty relative to the measured value.
Propagate Uncertainty
To effectively propagate uncertainty, we must look at the provisional rules of propagation (Do not worry, I will post a table with these rules in my next post). The calculation in our example is the quotient of two independent variables, so referring to the provisional rules of propagation for products and quotients, we should calculate the fractional uncertainty of each independent variable and combine them using the root sum of squares method.
The Result
With the completion of propagation, we now have an estimated value of measurement uncertainty. However, the estimation process may not be complete should we consider other factors that influence the measurement result, such as resolution, environmental conditions, etc.
I = 9.999140 A ± 0.00078 A
The goal of this post is to express the use and application of propagating uncertainty. Hopefully, this is beneficial to those seeking information and inspiration to learn more about it. Please leave comments on this post or feel free to contact me with your questions.