
Introduction
Have you ever considered using sensitivity coefficients when estimating measurement uncertainty?
Maybe you have seen sensitivity coefficients used in an uncertainty budget and wondered why they were used or how they were calculated.
If you answered yes to any of the above statements, this guide is for you.
Today, you are going to learn everything that you will ever need to know about using sensitivity coefficients to calculate uncertainty.
In this guide, you will learn:
• What are sensitivity coefficients,
• Why sensitivity coefficients are important,
• When you should use sensitivity coefficients,
• When you should not use sensitivity coefficients, and
• How to calculate sensitivity coefficients (step-by-step)
So, if you are interested in learning about sensitivity coefficients, keep reading. You have just found the ultimate guide for sensitivity coefficients and measurement uncertainty.
What are Sensitivity Coefficients
According to the Guide to the Expression of Uncertainty in Measurement (GUM), sensitivity coefficients are partial derivatives used to describe how the output estimate y varies with changes in the values of the input estimates x1, x2, …, xn.
Essentially, sensitivity coefficients show you how the variables in an equation or function are related to the calculated result.
When you change the value of variable x in an equation, it will have an effect on the magnitude of the result y.
This is helpful when estimating uncertainty so you can convert your uncertainty components to similar units of measurement.
Therefore, sensitivity coefficients are just a multiplier used to convert your uncertainty components to the right units and magnitude for your uncertainty analysis.
If you know the sensitivity coefficients for the variables in your measurement process, you can replicate the relationship when estimating uncertainty.
Why You Should Use Sensitivity Coefficients
According to the A2LA G104 Guide for Estimation of Measurement Uncertainty in Testing, uncertainty contributions must all be in the same units of measurement before they can be combined.
When deciding whether or not to use sensitivity coefficients, you should determine if your sources of uncertainty are quantified in the same units of measurement.
If they are, you do not need to use sensitivity coefficients.
If your contributors are in several different units of measurement, then you should consider using sensitivity coefficients.
However, you still have an option.
Instead of using sensitivity coefficients in your uncertainty budgets, you can convert the value of your individual uncertainty components before entering the data into your uncertainty budget.
Using this method, you do not need to use sensitivity coefficients.
For the sake of this guide, I am going to assume that you need to use sensitivity coefficients.
When You Should Use Sensitivity Coefficients
Use sensitivity coefficients when you need to convert uncertainty components to similar units of measurement for your analysis.
For example…
Imagine you have a set of steel gage blocks that has a coefficient of linear thermal expansion of 10.8 x 10-6 m/K. Now, imagine that you have a thermometer that monitors your working area and has a measurement uncertainty of 0.2°C.
How do you relate the uncertainty of the thermometer to the measurement uncertainty of the gage block?
With a sensitivity coefficient.
In this example, the coefficient of linear thermal expansion is your sensitivity coefficient. So, you do not need to calculate the sensitivity coefficient yourself.
Now, all you need to do is multiple the sensitivity coefficient and the uncertainty of your thermometer. The result will be the uncertainty component converted to meters (m) which is relatable to your analysis.

Alternatively, sensitivity coefficients can also be used to convert uncertainty components to the right order of magnitude.
For example…
Imagine you are performing an uncertainty analysis where the measurement results are in milli-meters (mm), but your uncertainty component is in meters (m).
Well, most people would just convert the uncertainty component to milli-meters (mm).
However, you can use sensitivity coefficients to accomplish this task for you.
By using a sensitivity coefficient of 1000, you are able to convert the uncertainty component from meters to milli-meters in your uncertainty budget.
This is another scenario of when to use sensitivity coefficients when estimating uncertainty.

Overall, this is how sensitivity coefficients work. They are used to convert your uncertainty components to units of measure and magnitude relative to your uncertainty analysis.
So, when you have sources of uncertainty that are in different units of measurement or order of magnitude, you should use sensitivity coefficients.
If you keep reading, I am going to teach you how to calculate sensitivity coefficients later in this guide.
When You Shouldn’t Use Sensitivity Coefficients
You do not need to use sensitivity coefficients if all of your input quantities or uncertainty contributors are all reported in the same unit of measure.
When all of your uncertainties are listed in the same units of measurement, you will just be wasting your time. So, don’t bother with sensitivity coefficients.
However, some uncertainty calculators require you to use sensitivity coefficients even if you do not need them.
When this happens, you must enter a value for the sensitivity coefficient or your uncertainty calculator may not function properly which may yield incorrect results or errors.
To avoid this problem, just use the value of one (i.e. 1) as your sensitivity coefficient.
It’s a quick and easy fix that will save you from a lot headaches.
In case you are wondering why you should use the value of one, look at the equation below and consider the following:
![]()
The uncertainty of your result y is calculated by multiplying the sensitivity coefficient and the uncertainty of your input variable x.
Any value multiplied by one will still equal the same value. So, using a sensitivity coefficient of one will allow you to calculate uncertainty and not affect the results.
To get a better understanding, take a look at the example below.
This is an uncertainty analysis for a laminar flow element where the measurement results are in standard cubic-centimeters per minute (sccm). Since the uncertainty related to repeatability is in the same units of measure (i.e. sccm), you do not need a sensitivity coefficient.
However, the uncertainty calculator in the image below requires you to enter a sensitivity coefficient. Therefore, you should use a value of one (i.e. 1).
Now, when the uncertainty calculator multiplies the sensitivity coefficient and the uncertainty value for repeatability, the result will not be affected.

So, when all of your uncertainty sources are quantified in the same units of measure as your measurement result, you do not need to use sensitivity coefficients.
However, if your uncertainty calculator requires you to use sensitivity coefficients, make sure to use a value of one in these situations.
How to Calculate Sensitivity Coefficients
Every once in a while, you will need to use a sensitivity coefficient when estimating uncertainty. Therefore, it is important for you to know how to calculate them.
In this section, I am going to show you how to calculate sensitivity coefficients for most basic scenarios.
However, it should be noted that some measurement functions can be rather complex and may require a more advanced method to calculate sensitivity coefficients.
This section is not going to teach you the advanced methods.
Instead, you are only going to learn how to perform the basic method. But, do not worry. Most of you will probably never encounter the rare need to use advanced methods.
With that disclosed, let’s get started.
To calculate sensitivity coefficients, you should compare the change in output variable y when changing the value of a particular input variable x while keeping the remaining variables constant.
Back in middle school algebra, you probably learned that the function of x equals y.
![]()
Knowing this principle, you can use the uncertainty or error of variable x to determine the change in the variable y.
When these values are known, you can use the equation below to calculate a sensitivity coefficient.
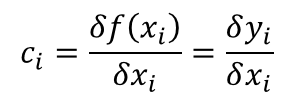
Essentially, all you need to do is divide the change in the variable y by the change in variable x.
If this explanation is confusing, I have broken the process down into nine easy steps that you can follow to calculate your first sensitivity coefficient.
Just follow the instructions below to calculate a sensitivity coefficient.
Calculating Sensitivity Coefficients Step-by-Step
1. Identify the measurement function or equation
The first step to calculating a sensitivity coefficient is to determine the function or equation that represents your measurement process.
2. Identify the variables in the equation.
Every variable that is part of the equation will be an input variable, x. The calculated result of the equation will always be the output variable, y.
3. Select a variable of interest.
Choose the variable in your equation that requires a sensitivity coefficient.
If more than one variable needs a sensitivity coefficient, only evaluate on one variable at a time.
4. Choose two values for your selected variable.
Pick two different values for your variable. Typically, you should pick a high and low value that represents the range of your measurement function.
Alternatively, you can select a single value for variable x and have the second value add the uncertainty of measurement to the original value of x.
Either method will work. So, choose the method that you are most comfortable performing.
5. Calculate and record the result using the first value.
Using the first value that you selected in step 4, plug it into your equation and calculate your first result for the output variable y.
If your equation has more than one input variable x, make sure to keep their values constant throughout this process. This is an important rule to remember when evaluating one variable at a time.
6. Calculate and record the result using the second value.
Next, plug the second value that you selected in step 4 into your equation, and calculate your second result for the output variable y.
7. Calculate the difference in your results, y.
Now that you have data, it is time to calculate your sensitivity coefficient.
Start by calculating the difference of the output variable y. Subtract the result of y in step 6 by the result of y in step 5.
8. Calculate the difference in your variable, x.
Then, calculate the difference of input variable x. Subtract the value of x in step 6 by the value of x in step 5.
9. Divide the difference in y by the difference in x.
Finally, divide the result of step 7 by the result of step 8.
This will be your sensitivity coefficient for the input variable x.
Bonus: Verify your results.
Afterward, make sure to verify your results. Just multiply your new sensitivity coefficient and the input variables that you selected in step 4.
You can use the equation below to help.
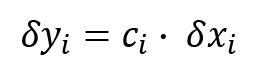
The result should be equal to the results calculated in steps 5 and 6.
If your results match, your sensitivity coefficient was correctly calculated. If not, you made a mistake and need to repeat the process until it works.
See How We Can Help Your Lab Get ISO/IEC 17025:2017 Accredited
- Uncertainty Budgets – let us estimate uncertainty for you.
- Custom QMS – we’ll create your quality manual, procedures, lists, and forms.
- Training – get online training that teaches you how to estimate uncertainty.
Examples of Calculating Sensitivity Coefficients
Now that you know how to calculate sensitivity coefficients, let’s look at some examples that demonstrate the process.
The examples in this section should help you grasp a visual concept of the written instructions in the previous section.
I have tried to make sure to give you practical examples that you can easily replicate and try for yourself.
The examples in the section will include:
1. DC Current Calibration Using Ohm’s Law
2. Gage Block Calibration and the Coefficient of Linear Thermal Expansion
3. Pressure Transducer Calibration with a 4 to 20 mA Output
4. Pressure Transducer Calibration with a 0 to 5 V Output
DC Current Calibration Using Ohm’s Law
If you have ever worked in electrical metrology, you should know Ohm’s Law and be very familiar with the PIE chart.
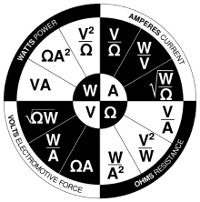
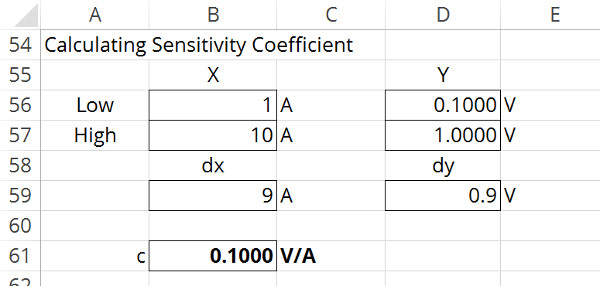
Using the principle of Ohm’s Law, imagine that you are indirectly measuring current using a 0.1 Ohm resistor and a digital multimeter.
At 1 ampere, you observe 0.1 volts on the digital multimeter.
At 10 amperes, you observe 1 volt on the digital multimeter.
Using your recorded data, calculate the difference of the two voltage measurements and the two current set points.
Then, divide the difference in volts by the difference in amperes.
The result is a sensitivity coefficient of 0.1 Volts per Ampere.
Gage Block Calibration and the Coefficient of Linear Thermal Expansion
If you have ever worked in dimensional metrology, you have probably heard of the coefficient of linear thermal expansion.
It can be used as a sensitivity coefficient. However, let’s verify the CTE by measuring the length of a steel gage block at two different temperatures.
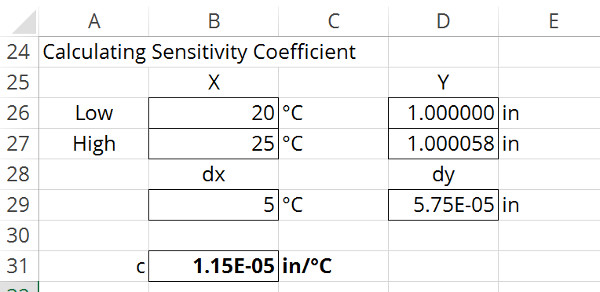
At 20°C, the gage block is approximately 1 inch.
At 25°C, the gage block is approximately 1.000058 inches.
Now that you have the measurement results, you will want to independently calculate the difference of both temperature and length.
Afterward, you will divide the difference in length by the difference in temperature.
The result is a sensitivity coefficient of 11.5 micro-inches per degree Celsius.
Pressure Transducer Calibration with a 4 to 20 mA Output
If you work in mechanical metrology and calibrate pressure transducers, I am confident that you have calibrated transducers that have a 4 to 20 mA output signal.
When it comes to estimating the uncertainty in measurement for these types of devices, I have observed a lot of people having issues with the conversion of uncertainty in pressure to the uncertainty in observed output signal.
In this example, I am going to show you how to find the sensitivity coefficient for these conversions.
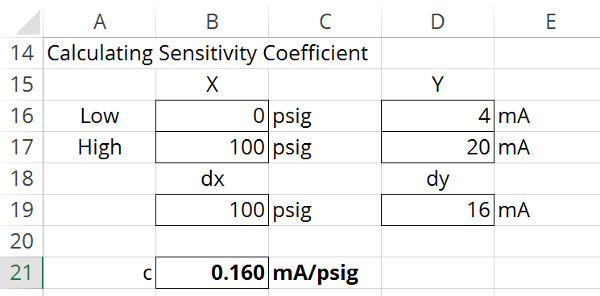
Imagine that you have a 0 to 100 psig pressure transducer that outputs a 4 to 20 mA signal.
At 0 psig, the transducer outputs a 4 mA signal.
At 100 psig, the transducer outputs a 20 mA signal.
By calculating the difference of each, you should have a difference of 100 psig and a difference of 16 mA respectively.
If you divide the difference of the output signal by the difference in pressure, you should have a sensitivity coefficient of 0.16 milli-Amps per psig.
Pressure Transducer Calibration with a 0 to 5 V Output
Similar to the previous example, some pressure transducers produce a voltage output signal rather than a current output signal.
Therefore, I am going to show you how to calculate the sensitivity coefficients for these devices.
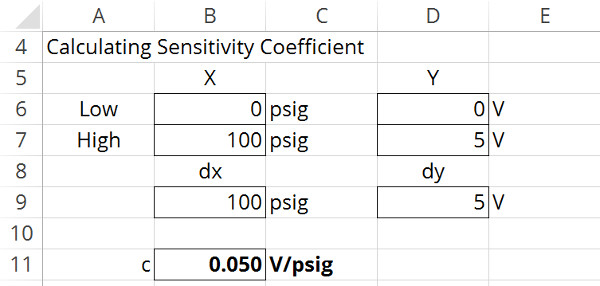
Imagine that you have a 0 to 100 psig pressure transducer that outputs a 0 to 5 V signal.
At 0 psig, the transducer outputs a 0 V signal.
At 100 psig, the transducer outputs a 5 V signal.
By calculating the difference of each, you should have a difference of 100 psig and a difference of 5 V respectively.
If you divide the difference of the output signal by the difference in pressure, you should have a sensitivity coefficient of 0.05 Volts per psig.
Sensitivity Coefficients and Uncertainty Budgets
Sensitivity coefficients are an important element in uncertainty analysis. Even though you may not always need to use them, your uncertainty calculator should offer you the option of using sensitivity coefficients.
If not, it is pretty easy to add sensitivity coefficients to an uncertainty calculator made in Excel.
Sensitivity coefficients should be used in your uncertainty calculation before you calculate the combined uncertainty.
So, you would multiple the sensitivity coefficient and the uncertainty value.
![]()
Take a look at the image below to see how the equation is used in my uncertainty calculator.
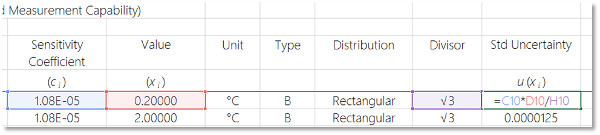
Looking at the example above, you will see that the sensitivity coefficient is placed into a column before and next to the uncertainty value.
If you look at the standard uncertainty column, you will notice that sensitivity coefficient and the uncertainty value are multiplied together before they are divided by the divisor.
Using this equation will ensure that your uncertainty value is properly converted to a standard uncertainty before the Root Sum of Squares (RSS) process.
If your uncertainty calculator does not include sensitivity coefficients, use the example and equation above to add them to your uncertainty budget.
Where to learn more about Sensitivity Coefficients
If you still wish to learn more about sensitivity coefficients and measurement uncertainty, I suggest that you read the following material to see if they can help answer your questions.
GUM
The Guide to the Expression of Uncertainty in Measurement
NIST SEMATECH
2.5.6. Uncertainty budgets and sensitivity coefficients
2.5.6.1. Sensitivity coefficients for measurements on the test item
Wikipedia
ISOBUDGETS
3 Ways to Combine Measurement Uncertainty With Different Units of Measurement
If these resources are not enough, leave a comment with your question and I will be glad to update this guide to answer your questions.
Conclusion
Sensitivity coefficients are an important element of estimating measurement uncertainty. Where practical, they should be included in your uncertainty budgets.
However, sensitivity coefficients are not needed for every uncertainty analysis. So make sure to only use them if you need them.
In this guide, you have learned everything that you need to know about sensitivity coefficients; what they are, when to use them, and how to calculate them. Plus, I have even given you a few practical examples.
Hopefully, you will find this guide useful if you ever need to calculate sensitivity coefficients.
So, make sure to give this process a try. Calculate a few sensitivity coefficients and post in the comments what you calculated sensitivity coefficients for or what questions you may have.





4 Comments