
Introduction
A couple of months ago, I wrote a 7 step guide to calculate measurement uncertainty. While the majority of feedback that I received informed me that the guide was helpful, I also received a few comments that the guide was missing more advanced topics; specifically, sensitivity coefficients.
Therefore, I decided to write an article to cover the use of sensitivity coefficients and other equivalent methods to combine uncertainty with different units of measure.
Combining Uncertainty
Combining measurement uncertainty with different units seems to be a common problem for many estimating uncertainty. However, there is not a lot of detailed information available in the free measurement uncertainty guides.
Most uncertainty guides cover the topic of sensitivity coefficients, but lack the use of examples to teach readers how to calculate and use sensitivity coefficients. I believe that writers of these guides tend to overlook that not all of their readers have Ph.D’s.
So, I decided to cover sensitivity coefficients and two other similar methods to combine uncertainty with different units of measure in this article. Furthermore, I decided to break down the process to the beginner level and give you examples to help you learn how to combine uncertainty with different measurement units.
Methods Used
In this article, I will cover how to combine uncertainty with different units using three different methods;
- Sensitivity Coefficients
- Fractional Uncertainty
- Mathematical Simulation
Now, fractional uncertainty and mathematical simulation are not typically covered in the majority of uncertainty guides that I have read. I first read about fractional uncertainty reading John Taylor’s “Introduction to Error Analysis.” Mathematical simulation is a process that I have not read about anywhere. So, tell me if I wrong when I say that this information is pretty exclusive to myself. However, I will say that it is pretty much inferred from just about every math textbook I have ever read for problem solving purposes.
The Example Problem
In this article, we will use the Ohm’s Law equation to demonstrate the application of each method. To keep it simple, we will use simple, made up values to make demonstration of use easier to understand.
For simplicity purposes, let’s assume that we are dealing with uncertainty values already reduced to standard deviation equivalents. Furthermore, the results calculated in the examples are only combined uncertainty calculations and will not be expanded to 95% confidence.
Below is the Ohm’s Law equation, where ‘E’ represents the value of voltage, ‘I’ represents the value for current, and ‘R’ represents the value for resistance. When we multiply current and resistance of a simple series electrical circuit (with one resistor), the result is the voltage present in the circuit.
If you think about calibrating a resistor, we apply a known value of current to a resistor with an unknown value and observe the voltage drop across the resistor. When we know the values of voltage and current, we can estimate the value of the resistor by dividing the voltage value by the current value.

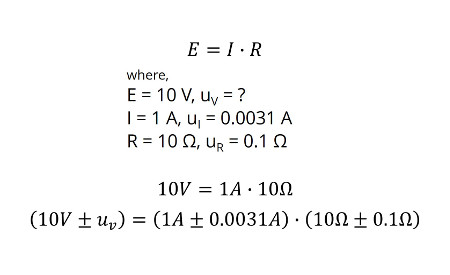
Combining uncertainty with different units really is not possible. You need to convert your uncertainty contributors to similar units.
Sensitivity Coefficients
Sensitivity coefficients show the relationship between an individual uncertainty contributor and the affect it has on the final result.
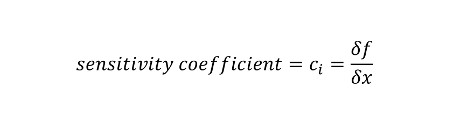
Using our Ohm’s Law example, I am going to show you how to calculate sensitivity coefficients. First, look at the Ohm’s Law equation and the equation for combining uncertainty.
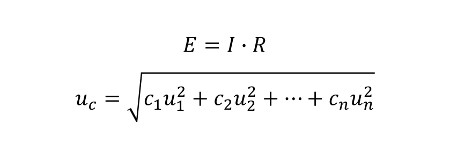
Now, use the two equations to develop the equation your will use for combining uncertainty. Notice that cI is your sensitivity coefficient for the current uncertainty and cR is your sensitivity coefficient for the resistance uncertainty. You should also be aware that uI is your current uncertainty and uR is your resistance uncertainty.
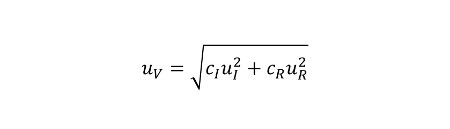
Next, look at the equation for calculating sensitivity coefficients. Notice that the sensitivity coefficient is the change or difference in our function of x (δf) divided by the difference in difference in the input variable, x (δx).
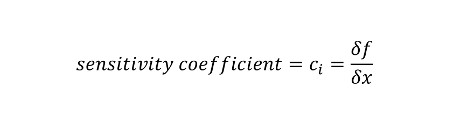
To start, let’s calculate the sensitivity coefficient for current. Looking at the equation below, you need to find the change in voltage caused by the change in current.
Earlier, I gave you the change in current earlier when I provided you the value for the current uncertainty. You will use the current uncertainty in the Ohm’s Law equation to find the change in voltage.
Here is our original equation.
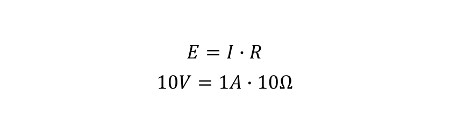
Here is the equation modified to solve for the change in the voltage. By inputting the known values, we can calculate the change in the calculated voltage.
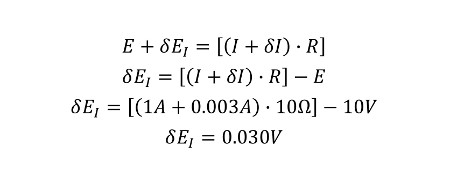
Now that you know the change in voltage caused by the change in current, we can calculate the sensitivity coefficient for the current uncertainty. Notice that the result is in units volts per ampere. This is to convert our current uncertainty value in amperes to volts, so you will combine similar units instead of different units.
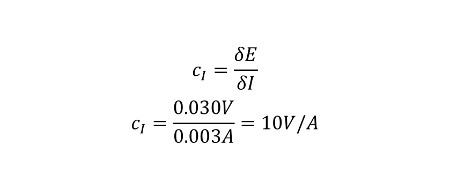
Next, you must repeat this process to calculate the change in voltage caused by the change in resistance.
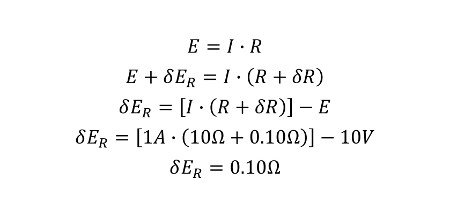
Afterward, use the results to determine the sensitivity coefficient for resistance uncertainty in units Volts per Ohm.
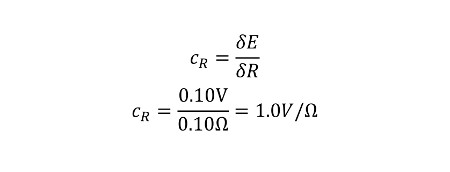
With your newly calculated sensitivity coefficients, it is time to combine uncertainty. Simply plug in all the known values into the equation below and calculate the combined uncertainty for voltage. Notice that your sensitivity coefficients convert your uncertainty values to volts so you can combine similar units of measure.
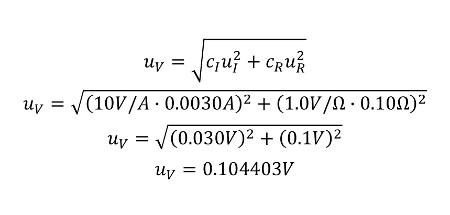
You have just calculated sensitivity coefficients, and combined uncertainty for contributors with different units of measure. I know it seems like a lot of work, but it is a necessary process to properly combine uncertainty using sensitivity coefficients.
Let’s recap the process.
1. Identify the equation
2. Change the input variables (x), one at a time, to calculate the change in the output variable (y).
3. Use the change in the output value (y) to calculate the sensitivity coefficient (c).
4. Repeat for each variable.
5. Calculate the combined uncertainty.
Fractional Uncertainty
Another method of combining uncertainty with different units of measure is fractional uncertainty. I read about this method in John Taylor’s book, “Introduction to Error Analysis.” Essentially, you will convert your uncertainty contributors to fractional equivalents in percentage before combining them.
This is the equation for calculating fractional uncertainty. You find the change in x and divide it by the absolute value of x to calculate fractional uncertainty in percentage.

Start with the combined uncertainty equation from our example. Next, input the fractional uncertainty equation for each uncertainty contributor. Then, use the given values from the example and input them into the equation.
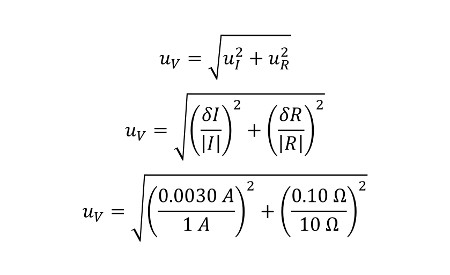
After solving the equation, you have two percentage values. One for current uncertainty and one for resistance uncertainty.
Finally, combine the values using the root sum of squares method (RSS). The result should be a combined uncertainty value in percentage. To convert the value to Volts, multiple the value of voltage by the uncertainty value in percentage to find the value of voltage uncertainty.
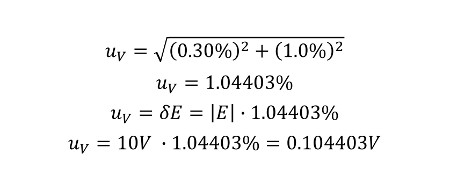
Notice that this process requires less problem solving because we already know all of the values for each variable.
Let’s recap the process.
1. Identify the equation
2. Calculate the fractional uncertainty for each contributor.
3. Calculate the combined uncertainty.
4. Convert the result to the desired unit of measure.
Mathematical Simulation
The final method that I will tell you about is simulation. In this method, you will mathematically simulate the output value of an equation by inputting different values for the variable ‘x.’
This method is very helpful when trying to estimate the magnitude of uncertainty influences that you are not able to test. Instead, you can use mathematical simulation to estimate the change in the measurement result.
Similar to finding your sensitivity coefficients, you will use the given values for current and it’s uncertainty in the equation below to calculate the change in voltage. The calculated result is your new value for current uncertainty in volts. Next, repeat the process for resistance.
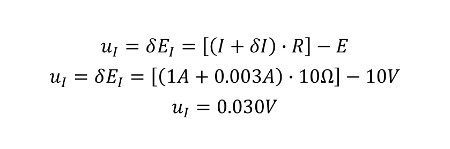
Use the given values for resistance and it’s uncertainty in the equation below to calculate the change in voltage. The calculated result is your new value for resistance uncertainty in volts.
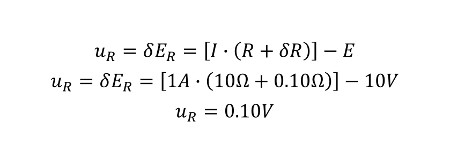
Now that you have calculated the changes in voltage caused by the uncertainty of current and resistance, it is time to use the root sum of squares equation to combine uncertainty.
Input the two values calculated in the two previous equations and calculate the combined uncertainty for voltage. The result will be uncertainty of our measurement process.
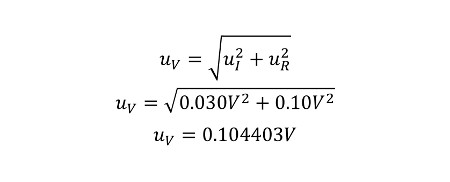
Notice that this process is similar to the finding your sensitivity coefficients, but eliminates the extra steps required to calculate sensitivity coefficients. It requires less problem solving because we already know all of the values for each variable. Essentially, it saves you time and reduces the chance of you making a mistake caused by the additional calculations needed to find sensitivity coefficients.
Let’s recap the process.
1. Identify the equation
2. Change the input variables (x), one at a time, to calculate the change in the output variable (y).
3. Use the change in the output value as the magnitude of your uncertainty’s influence.
4. Repeat for each variable.
5. Calculate the combined uncertainty.
Comparison of Methods
To compare the methods I have shown you, let’s evaluate the calculated results, the level of difficulty and the time needed to complete each method.
Looking at the final calculations of each method, you should notice that the result of each method is the same. First, this should show you that I calculated everything correctly. Second, it should assure you that you can use any one of these methods without fear of additional uncertainty in your calculated result.
When assessing the difficultly of these methods, you should consider the ease of use. After all, you will be the one using this method. Therefore, you should select the method that is easiest for you to use in your uncertainty analysis. For me, I like to use mathematical simulation. However, I would anticipate that most people will like to use the fractional uncertainty method. It is quite easy to use!
If your time is precious to you, select the method that is the quickest for you to complete. After reviewing each one of these methods, I believe that fractional uncertainty is the fastest method to complete. There are just fewer steps to perform! This could also infer that the method should be easy for beginners to learn and apply.
So, if you are a beginner to uncertainty analysis and need to combine uncertainty factors that have different units of measure, I recommend that you give the fractional uncertainty method a try first.
After you try it, give me your opinion in the comment section below. I want to know what method worked best for you. Also, other readers would like to know which method you found to be the best.
Conclusion
In this article, I have taught you three methods to combine measurement uncertainty when different units of measure are involved. Additionally, I have demonstrated how perform each method with guidance and examples. Furthermore, I have evaluated the three methods and offered my personnel recommendations for the preferred method that you should use.
Now, you should try to perform these methods yourself and leave a comment below for which method you prefer to use and why. If you have problems and need help, ask your question in the comment section below. I will be glad to help and answer your questions.





12 Comments